Lab4

Alternerende sum

I filen alternating_sum.py opprett funksjonen alternate_sign_sum som tar inn en liste med tall nums som parameter. Funksjonen skal regne ut den alternerende summen av tallene i listen nums (nums[0] - nums[1] + nums[2] - nums[3] … nums[n-1]). Funksjonen skal være ikke-destruktiv.

Test deg selv:

def test_alternate_sign_sum():
    print('Tester alternate_sign_sum...', end=' ', flush=True)
    assert 3 == alternate_sign_sum([1, 2, 3, 4, 5])
    assert 30 == alternate_sign_sum([10, 20, 30, 40, 50])

    a = [-10, 20, -30, 40, -50]
    assert -150 == alternate_sign_sum(a)
    assert [-10, 20, -30, 40, -50] == a  # Sjekk at funksjon ikke er destruktiv
    print('OK')

Mutasjon

I denne laben skal vi jobbe med lister. Funksjonene vi skal skrive i denne laben er ofte beskrevet som enten destruktive eller ikke-destruktive. For å forstå forskjellen, varmer vi opp med litt teori: les deg opp om mutasjon, alias og destruktive funksjoner i notatene om lister. Under følger også et kort sammendrag:

Å mutere et objekt innebærer å endre på objektetet i minnet.

Lister kan muteres. For eksempel, hvis vi har en liste

a = [42, 95, 66]
og ønsker å legge til en ny verdi i listen
a += [77, 88]

så er dette en endring som er slik at selve liste-objektet i minnet blir endret. Variabelen endres altså ikke, den peker fremdeles på akkurat samme objekt; det er bare at objektet i seg selv har blitt endret. Vi sier at listen har blitt mutert.

---

Ikke alle typer objekter kan muteres. For eksempel kan ikke str, int, bool eller float muteres. Når man gjør en operasjon for å regne ut en ny verdi av disse typene, vil det alltid opprettes et nytt objekt i minnet. For eksempel, hvis vi har en streng

s = 'abc'
og ønsker å legge til flere tegn i strengen
s += 'def'

så vil det opprettes et nytt objekt 'abcdef' og variabelen s blir endret til å peke på det nye objektet.

To variabler er aliaser dersom de peker på det samme objektet.

For eksempel,

a = [1, 2, 3] b = a
vil innebære at a og b er aliaser, mens
a = [1, 2, 3] b = [1, 2, 3]

vil innebære at a og b ikke er aliaser. Selv om objektene i det sistnevnt tilfelle er like, er det likevel hver sine objekter med ulik plassering i minnet.

---

En vanlig form for alias oppstår når vi kaller en funksjon med en variabel som argument. Da vil parameteren (en lokal variabel i funksjonskallet) være et alias med variabelen benyttet som argumentet i kodeblokken som kallet funksjonen. Hvis parameteren muteres, vil altså verdien som variabelen i hovedprogrammet peker på også bli endret.

Selve oppgaven: for hver av funksjonene under, forklar hva funksjonen gjør og avgjør om funksjonen er destruktiv eller ikke-destruktiv. Du kan anta at input er forventet å være en liste med tall. Du kan gjerne prøve ut funksjonen (kall den med noen input-verdier du tror egner seg følg med på hva som skjer i debuggeren). Det er ikke sikkert at alle funksjonene fungerer etter hensikten, i så fall skriv ned hva som er feil i forklaringen din.

def funA(a):
    while 3 in a:
        a.remove(3)

def funB(a):
    ra = []
    rb = []
    for x in a:
        if x < 10:
            ra.append(x)
        else:
            rb.append(x)
    return ra + rb

def funC(a):
    n = len(a)
    for i in range(n):
        a[i] = a[i] + 3
    return a

def funD(a):
    n = len(a)
    r = []
    for i in range(n):
        if i % 2 == 0:
            r.append(a[i])
    return r

def funE(a):
    i = len(a) - 1
    c = 0
    while i >= 0:
        if a[i] < 3:
            a.pop(i)
            c += 1
        i -= 1
    return c

def funE(a):
    mi = None
    for x in a:
        if mi is None or x < mi:
            mi = x

Svarene dine skal du levere som en python-fil mutasjonsquiz.py som kun inneholder bestemte variabler. Kopier og fyll ut:

funA_is_destructive = ... # True eller False
funA_description = '' # Skriv din forklaring inne i strengen

funB_is_destructive = ...
funB_description = ''

funC_is_destructive = ...
funC_description = ''

funD_is_destructive = ...
funD_description = ''

funE_is_destructive = ...
funE_description = ''

funF_is_destructive = ...
funF_description = ''

Merk at det kun er svarene dine på _is_destructive som rettes automatisk. Når det gjelder forklaringene dine kan du spørre en gruppeleder om du har rett eller feil.

Dobling

I denne oppgaven skal du skrive funksjoner som dobler alle tall i en liste. I del A skal du skrive en destruktiv funksjon, mens i del B skal du skrive en ikke-destruktiv funksjon. Begge funksjonene skal du skrive i samme fil, duplicate.py.

Del A

Skriv en funksjon duplicate med en parameter numbers. Du kan anta at numbers vil være en liste med tall. La funksjonen mutere listen slik at alle tallverdier blir dobbelt så store.

def test_duplicate():
    print('Testing duplicate...', end=' ', flush=True)

    # Test 1
    arg = [2, 3, 10, 3, 4]
    return_val = duplicate(arg)
    expected = [4, 6, 20, 6, 8]
    assert return_val is None
    assert expected == arg

    # Test 2
    arg = [3, 2]
    duplicate(arg)
    duplicate(arg)
    expected = [12, 8]
    assert expected == arg

    print('OK')

Del B

Skriv en funksjon duplicated med en parameter numbers. Du kan anta at numbers vil være en liste med tall. La funksjonen returnere en ny liste med tallverdier som er dobbelt så store.

def test_duplicated():
    print('Testing duplicated...', end=' ', flush=True)

    # Test 1
    arg = [2, 3, 10, 3, 4]
    return_val = duplicated(arg)
    expected = [4, 6, 20, 6, 8]
    assert return_val == expected
    assert arg == [2, 3, 10, 3, 4]

    # Test 2
    arg = [3, 2]
    return_val = duplicated(duplicated(arg))
    expected = [12, 8]
    assert return_val == expected
    assert arg == [3, 2]

    print('OK')

Gressklipper

Du jobber som gressklipper og har fått i oppgave å klippe gresset i en hage. Eieren av hagen er veldig interessert i å vite den nøyaktige høyden på gresset etter at det er klippet. Du har fått en liste heights som eieren har laget over høyden på gresset på forskjellige steder i hagen. Du har også fått en høyde max_height som beskriver hvor høyt gresset maksimalt skal være. Det betyr at hvis gresset er høyere enn denne høyden, skal det klippes ned til denne høyden.

I en fil clip_grass.py, lag en funksjon clip_grass som tar inn en liste av høyder heights og en høyde max_height. Funksjonen skal mutere listen heights slik at alle høyder som er større enn max_height blir klippet ned til max_height. Fordi funksjonen er destruktiv, trenger den ikke returnere noe.

Som et eksempel, hvis du har følgende liste med høyder:

[1, 2, 3, 4, 5]

Og maksimal høyde er 3, så vil listen etter klipping være:

[1, 2, 3, 3, 3]

Test deg selv:

def test_clip_grass():
    print('Testing clip_grass... ', end='')
    # Case 1
    heights = [1, 2, 3, 4, 5]
    clip_grass(heights, 3)
    assert [1, 2, 3, 3, 3] == heights

    # Case 2
    heights = [1, 2, 3, 3, 3]
    clip_grass(heights, 3)
    assert [1, 2, 3, 3, 3] == heights

    # Case 3
    heights = [10, 20, 200, 20, 400]
    clip_grass(heights, 25)
    assert [10, 20, 25, 20, 25] == heights
    print('OK')

if __name__ == '__main__':
    test_clip_grass()

Voksne og barn

I denne oppgaven skal du skrive funksjoner som filtrerer en liste av objekter. I del A skal du skrive en destruktiv funksjon, mens i del B skal du skrive en ikke-destruktiv funksjon. Begge funksjonene skal du skrive i samme fil, adults_and_children.py.

Del A

Skriv en funksjon remove_children med en parameter people. Du kan anta at people vil være en liste med oppslagsverk, der alle oppslagsverk har en nøkkel 'age' hvor tilhørende verdi er et tall. La funksjonen mutere listen slik at alle personer med alder under 18 år fjernes.

def test_remove_children():
    print('Testing remove_children...', end=' ', flush=True)

    # Test 1
    arg = [
        {'name': 'Ole', 'age': 18},
        {'name': 'Ida', 'age': 12},
        {'name': 'Eva', 'age': 13},
        {'name': 'Liv', 'age': 37},
        {'name': 'Adam', 'age': 8}
    ]
    return_val = remove_children(arg)
    expected = [
        {'name': 'Ole', 'age': 18},
        {'name': 'Liv', 'age': 37}
    ]
    assert return_val is None
    assert expected == arg

    # Test 2
    arg = [
        {'name': 'Per', 'age': 8},
        {'name': 'Pål', 'age': 6},
        {'name': 'Espen', 'age': 3}
    ]
    remove_children(arg)
    expected = []
    assert expected == arg

    print('OK')

PS! Å fjerne elementer fra en liste inni en løkke krever at man har tungen rett i munnen. Ta en nøye kikk på notatene om løkker over lister og se om du finner noen relevante eksempler.

Del B

Skriv en funksjon get_adults med en parameter people. Du kan anta at people vil være en liste med oppslagsverk, der alle oppslagsverk har en nøkkel 'age' hvor tilhørende verdi er et tall. La funksjonen returnere en ny liste med alle personer som er 18 år eller eldre.

def test_get_adults():
    print('Testing get_adults...', end=' ', flush=True)

    # Test 1
    arg = [
        {'name': 'Ole', 'age': 18},
        {'name': 'Ida', 'age': 12},
        {'name': 'Eva', 'age': 13},
        {'name': 'Liv', 'age': 37},
        {'name': 'Adam', 'age': 8}
    ]
    return_val = get_adults(arg)
    expected = [
        {'name': 'Ole', 'age': 18},
        {'name': 'Liv', 'age': 37}
    ]
    assert return_val == expected
    assert arg == [
        {'name': 'Ole', 'age': 18},
        {'name': 'Ida', 'age': 12},
        {'name': 'Eva', 'age': 13},
        {'name': 'Liv', 'age': 37},
        {'name': 'Adam', 'age': 8}
    ]

    # Test 2
    arg = [
        {'name': 'Per', 'age': 8},
        {'name': 'Pål', 'age': 6},
        {'name': 'Espen', 'age': 3}
    ]
    actual = get_adults(arg)
    expected = []
    assert expected == actual

    print('OK')

Dobling i 2D

En to-dimensjonell liste er egentlig bare en liste som inneholder lister. Det er mange ulike data som naturlig kan lagres som 2D-lister, slik som for eksempel matriser, regneark, data knyttet til kart og lignende.

I denne oppgaven skal vi skrive funksjoner for å doble alle verdier i en 2D-liste. I del A skal du skrive en destruktiv funksjon, mens i del B skal du skrive en ikke-destruktiv funksjon. Begge funksjonene skal du skrive i samme fil, duplicate.py (altså samme fil som i en tidligere oppgave).

Del A

Skriv en funksjon duplicate_2d med en parameter grid. Du kan anta at grid vil være en 2D-liste med tall. La funksjonen mutere 2D-listen slik at tallverdiene dobles.

def test_duplicate_2d():
    print('Testing duplicate_2d...', end=' ', flush=True)

    # Test 1
    arg = [
        [2, 3, 4],
        [4, 1, 0]
    ]
    return_val = duplicate_2d(arg)
    expected = [
        [4, 6, 8],
        [8, 2, 0]
    ]
    assert return_val is None
    assert expected == arg

    # Test 2
    arg = [[3, 2], [2, 1], [1, 0]]
    duplicate_2d(arg)
    duplicate_2d(arg)
    expected = [[12, 8], [8, 4], [4, 0]]
    assert expected == arg

    print('OK')

Del B

Skriv en funksjon duplicated_2d med en parameter grid. Du kan anta at grid vil være en 2D-liste med tall. La funksjonen returnere en ny 2D-liste med tallverdier som er dobbelt så store.

def test_duplicated_2d():
    print('Testing duplicated_2d...', end=' ', flush=True)

    # Test 1
    arg = [
        [2, 3, 4],
        [4, 1, 0]
    ]
    return_val = duplicated_2d(arg)
    expected = [
        [4, 6, 8],
        [8, 2, 0]
    ]
    assert return_val == expected
    assert arg == [
        [2, 3, 4],
        [4, 1, 0]
    ]

    # Test 2
    arg = [[3, 2], [2, 1], [1, 0]]
    return_val = duplicated_2d(duplicated_2d(arg))
    expected = [[12, 8], [8, 4], [4, 0]]
    assert return_val == expected
    assert arg == [[3, 2], [2, 1], [1, 0]]

    print('OK')

Flagg

I filen multicolored_flag.py opprett en funksjon draw_multicolored_flag med seks parametere: canvas, x1, y1, x2, y2, colors. Parameteren colors skal være en liste med strenger som representerer farger. Funksjonen skal tegne et flagg med vertikale striper på canvas med øvre venstre hjørne i punktet \((x_1, y_1)\) og nedre høyre hjørne i punktet \((x_2, y_2)\). Flagget skal ha like mange striper som det er farger i listen colors og hver oppføring i listen skal reflekteres i fargen på tilsvarende stripe. Første stripe skal altså ha farge colors[0], andre stripe skal ha farge colors[1], osv. Funksjonen trenger ikke å ha noen returverdi.

Merk: I filen multicolored_flag.py skal du ikke importere noe, og du skal heller ikke kalle på display-funksjonen. For å teste koden, opprett i stedet en separat fil multicolored_flag_test.py i samme mappe som multicolored_flag.py og kopier inn koden under. Når du kjører multicolored_flag_test.py, skal det tegnes tre flagg på skjermen som vist under:

from uib_inf100_graphics.simple import canvas, display
from multicolored_flag import draw_multicolored_flag

draw_multicolored_flag(canvas, 125, 135, 275, 265, ["red", "orange", "yellow", "green", "blue", "purple"])
draw_multicolored_flag(canvas, 10, 10, 40, 36, ["black", "yellow", "red"])
draw_multicolored_flag(canvas, 10, 340, 390, 360, ["black", "white", "black","black", "white", "black","black", "white", "black"])

display(canvas)

PS: Når du kaller på canvas.create_rectangle, legg til outline="" i argumentlisten. Da unngår du at det tegnes en svart ramme rundt rektangelet.

Pythonesia

Om du ikke allerede kan indeksering av 2d-lister veldig godt, anbefaler vi at du benytter fremgangsmåten og pseudokoden under for å se hvordan du kan iterere over en 2d-liste.

Du er med i en ekspedisjon til Pythonesia, et land som er kjent for sine mange rutenett av tall. Noe du har lest i reisehåndboken er at det er en gammel legende om at det finnes skatter gjemt under et av rutenettene i Pythonesia. Det er nemlig gjemt en skatt under alle ruter hvor radnummeret, kolonnenummeret og verdien i ruten (rad, kolonne) summerer til et spesielt tall. Du tenker du kan bruke dine programmeringsferdigheter til å finne posisjonene til disse skattene.

I en fil find_treasure.py, lag en funksjon find_treasure som tar inn en 2D-liste grid og et tall target_sum. Funksjonen skal returnere en liste av koordinater [row,col] i rutenettet hvor summen av rad, kolonne og verdi er lik target_sum. Hvis det ikke finnes noen slike skatter, skal funksjonen returnere en tom liste.

For eksempel, hvis du har følgende rutenett:

[ 
    [1, 2, 3],
    [4, 5, 6],
    [7, 8, 9],
]

og target_sum er 5, så skal funksjonen returnere [[0, 2], [1, 0]] siden på rad 0, kolonne 2, så er summen 0 + 2 + 3 = 5, og på rad 1, kolonne 0, så er summen 1 + 0 + 4 = 5. Se bilder under for visualisering:

def find_treasure(grid, target_sum):
    ... # Din kode her

    # opprett en tom liste `treasures` som skal inneholde koordinatene til skattene.
    # definer en variabel `rows` som er antall rader i rutenettet
    # definer en variabel `cols` som er antall kolonner i rutenettet

    # lag en ytre løkke `for row in range(rows)`
        # lag en indre løkke `for col in range(cols)`
            # hent ut verdi til denne posisjonen
            # sjekk om summen av radnummer, kolonnenummer og verdi er lik `target_sum`
                # hvis det er tilfellet, legg koordinatene ``[row, col]`` til `treasures`
    
    # returner `treasures`

Test deg selv:

def test_find_treasure():
    print('Testing find_treasure... ', end='')
    # Test 1
    grid = [
        [1, 2, 3],
        [4, 5, 6],
        [7, 8, 9],
    ]
    target_value = 5
    actual = find_treasure(grid, target_value)
    expected = [[0, 2], [1, 0]]
    assert expected == actual

    # Test 2
    actual = find_treasure([[1, 2], [3, 4]], 3)
    expected = [[0, 1]]
    assert expected == actual

    # Test 3
    actual = find_treasure([[1, 2], [3, 4]], 1)
    expected = [[0, 0]]
    assert expected == actual

    # Test 4
    actual = find_treasure([[1, 2], [3, 4]], 1000)
    expected = []
    assert expected == actual

    print('OK')

Minste absolutt-forskjell

I filen least_difference.py skriv funksjonen smallest_absolute_difference som har en liste med tall a som parameter. Funksjonen skal returnerer den minste absolutt-verdi som er forskjellen mellom to tall i listen a.

Test deg selv:

def test_smallest_absolute_difference():
    print('Tester smallest_absolute_difference... ', end='')
    assert 1 == smallest_absolute_difference([1, 20, 4, 19, -5, 99])  # 20-19
    assert 6 == smallest_absolute_difference([67, 19, 40, -5, 1])  # 1-(-5)
    assert 0 == smallest_absolute_difference([2, 1, 4, 1, 5, 6])  #1-1
    a = [50, 40, 70, 33]
    assert 7 == smallest_absolute_difference(a)
    assert [50, 40, 70, 33] == a  # Sjekker at funksjonen ikke er destruktiv
    print('OK')

Integraler

Denne oppgaven består av fire deler. Skriv alle funksjoner til de fire delene (A-D) i én felles fil, integrals.py.

Del A

I matematikken kan en funksjon for eksempel være definert som \(g(x) = \frac{1}{8}x^2 - 2x + 10\). La oss modellere denne matematiske funksjonen som en programmeringsfunksjon:

• I filen integrals.py, opprett en funksjon g som har en parameter x og som regner ut verdien av \(\frac{1}{8}x^2 - 2x + 10\) for den gitte verdien av x.

For eksempel skal et kall til g(8.0) returnere verdien 2.0, og et kall til g(4.0) skal returnere verdien 4.0.

Test deg selv:

def almost_equals(a, b):
    return abs(a - b) < 0.0000001

def test_g():
    print('Tester g... ', end='')
    # Første test
    x = 8.0
    actual = g(x)
    expected = 2.0
    assert almost_equals(expected, actual)

    # Flere tester
    assert almost_equals(4.0, g(4.0))
    assert almost_equals(10.0, g(0.0))
    print('OK')

if __name__ == '__main__':
    test_g()

Del B

I denne oppgaven skal vi regne ut en tilnærming for arealet under funksjonen \(g\) (fra del A) mellom to gitte punkter \(x_\text{lo}\) og \(x_\text{hi}\) på x-aksen. Vi antar at \(x_\text{lo} \leq x_\text{hi}\), og i denne omgang antar vi også at \(x_\text{lo}\) og \(x_\text{hi}\) er heltall.

For å gjøre vår tilnærming, skal vi enkelt nok regne ut summen av g(x_i) for alle heltalls-verdier \(x_i\) fra og med \(x_\text{lo}\) opp til (og ikke inkludert) \(x_\text{hi}\). For eksempel, dersom \(x_\text{lo} = 3\) og \(x_\text{hi} = 7\), er vi interessert i å vite hva summen \(g(3) + g(4) + g(5) + g(6)\) blir.

• I filen integrals.py, opprett en funksjon approx_area_under_g med parametre x_lo og x_hi som returnerer summen av g(x_i) for alle heltall x_i fra og med x_lo opp til x_hi.

Test deg selv (legg også inn et korresponderende funksjonskall i if __name__ == '__main__' -blokken din på slutten av filen):

def test_approx_area_under_g():
    print('Tester approx_area_under_g... ', end='')
    # Første test
    x_lo = 4
    x_hi = 5
    actual = approx_area_under_g(x_lo, x_hi) 
    expected = 4.0  # skal gi oss kun g(4), som altså er 4.0
    assert almost_equals(expected, actual)

    # Flere tester
    assert almost_equals(3.125, approx_area_under_g(5, 6)) # g(5)
    assert almost_equals(7.125, approx_area_under_g(4, 6)) # g(4)+g(5)
    assert almost_equals(23.75, approx_area_under_g(1, 5)) # g(1)+g(2)+g(3)+g(4)
    print('OK')

Del C

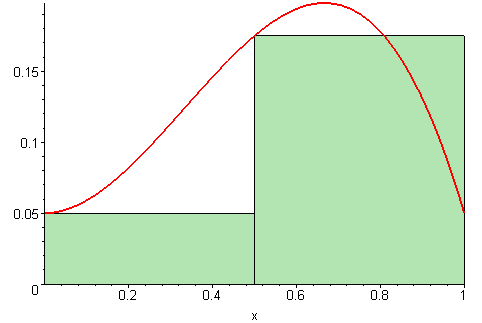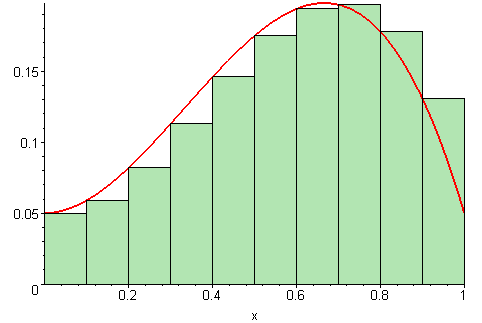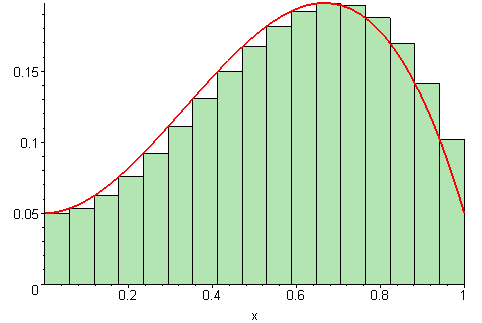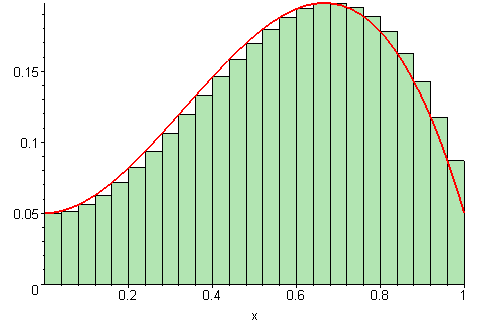
Estimatet for arealet vi regnet ut i forrige deloppgave er bare et estimat, siden vi later som funksjonen går i «trapper» i stedet for å være kontinuerlig, slik den egentlig er. For å gjøre estimatet vårt bedre, kan vi redusere bredden på hvert trappetrinn. Jo smalere trappetrinn vi velger, jo bedre blir estimatet vårt for arealet.

På figuren under vises det ulike bredder på trappetrinnene. Jo flere trappetrinn, jo mer nøyaktig vil arealet av det grønne området (som vi regner ut) stemme med det faktiske arealet under grafen (den røde streken).

Illustrasjon av 09glasgow09, CC BY-SA 3.0.

I denne oppgaven skal vi forbedre estimatet for arealet under grafen ved å la dem som kaller funksjonen vår bestemme hvor mange trappetrinn de ønsker å benytte. Dette kalles en (venstresidet) Riemann sum.¹

• I filen integrals.py, opprett en funksjon riemann_sum_g med parametre x_lo, x_hi og n. Funksjonen skal returnere en tilnærming av arealet under grafen g fra oppgave A basert på n antall trappetrinn.

• På samme måte som i del B skal vi oppdatere en løpende total i en løkke.

• På samme måte som i oppgaven «Oppdelt linjestykke» fra lab 3, skal vi dele opp linjestykket \([x_\text{lo}, x_\text{hi}]\) i \(n\) like store biter. Bruk gjerne funksjonen din derfra her også.

• Arealet ett trappetrinn bidrar med er produktet av bredden og høyden på trappetrinnet.

I del B var bredden alltid 1, så der forenklet vi det litt og benyttet oss kun av høyden – her i del C trenger vi derimot å ta med oss også trinnets bredde i beregningen.

Merk: i denne oppgaven vet du allerede før løkken starter hvor mange iterasjoner løkken skal ha (nemlig n). Derfor bør du velge en for-løkke, og ikke en while-løkke. I denne oppgaven kan faktisk det å velge en while-løkke, i kombinasjon med avrundingsfeil som alltid vil skje når vi jobber med flyttall, gjøre at du får helt feil svar!

Test deg selv:

def test_riemann_sum_g():
    print('Tester riemann_sum_g... ', end='')
    assert almost_equals(7.125, riemann_sum_g(4, 6, 2))
    assert almost_equals(6.71875, riemann_sum_g(4, 6, 4))
    assert almost_equals(6.3348335, riemann_sum_g(4, 6, 1000))

    assert almost_equals(23.75, riemann_sum_g(1, 5, 4))
    assert almost_equals(22.4375, riemann_sum_g(1, 5, 8))
    assert almost_equals(21.166676666, riemann_sum_g(1, 5, 1_000_000))
    print('OK')

Del D

Vi ønsker nå å regne ut arealet under flere grafer enn bare \(g\). Når alt kommer til alt er funksjonen \(g(x) = \frac{1}{8}x^2 - 2x + 10\) relativt obskur.

Opprett en funksjon riemann_sum med parametre f, x_lo, x_hi og n. Funksjonen skal returnere en tilnærming av arealet under grafen f mellom x_lo og x_hi basert på n antall trappetrinn. Koden vil være helt identisk med forrige deloppgave, bortsett fra at du kaller f(x_i) istedet for g(x_i) inne i løkken.

Test deg selv:

def test_riemann_sum():
    test_riemann_sum_using_g()
    test_riemann_sum_using_square()
    test_riemann_sum_using_linear()

def test_riemann_sum_using_g():
    print('Tester riemann_sum med funksjonen g... ', end='')
    assert almost_equals(7.125, riemann_sum(g, 4, 6, 2))
    assert almost_equals(6.71875, riemann_sum(g, 4, 6, 4))
    assert almost_equals(6.3348335, riemann_sum(g, 4, 6, 1000))

    assert almost_equals(23.75, riemann_sum(g, 1, 5, 4))
    assert almost_equals(22.4375, riemann_sum(g, 1, 5, 8))
    assert almost_equals(21.166676666, riemann_sum(g, 1, 5, 1_000_000))
    print('OK')

def test_riemann_sum_using_square():
    def square(x):
        return x**2

    ## Arealet under grafen square(x) = x**2 mellom 1 og 3
    ## Eksakt svar  er 8 + 2/3, altså 8.66666666....
    ## Merk at vi kommer gradvis nærmere eksakt svar ved å øke n
    print('Tester riemann_sum med funksjonen square... ', end='')
    assert almost_equals(5.0, riemann_sum(square, 1, 3, 2))
    assert almost_equals(7.88, riemann_sum(square, 1, 3, 10))
    assert almost_equals(8.5868, riemann_sum(square, 1, 3, 100))
    print('OK')

def test_riemann_sum_using_linear():
    def linear(x):
        return x

    ## Arealet under grafen for funksjonen f(x) = x mellom 2 og 4
    ## Eksakt svar er 6.
    ## Merk at vi kommer gradvis nærmere riktig svar ved å øke n
    print('Tester riemann_sum med funksjonen linear... ', end='')
    assert almost_equals(5.0, riemann_sum(linear, 2, 4, 2))
    assert almost_equals(5.5, riemann_sum(linear, 2, 4, 4))
    assert almost_equals(5.998046875, riemann_sum(linear, 2, 4, 1024))
    print('OK')

Rutenett

I filen colored_grid.py opprett en funksjon draw_grid som tar in følgende parametre: canvas, x1, y1, x2, y2, color_grid. Parameteren color_grid er en 2D-liste med strenger som representerer farger. Funksjonen skal tegne et rutenett med farger med øvre venstre hjørne i punktet \((x_1, y_1)\) og nedre høyre hjørne i punktet \((x_2, y_2)\). Fargene i listen color_grid skal reflektere fargen på rutene i tilsvarende posisjon (se eksempelkjøringen). Funksjonen trenger ikke å ha noen returverdi.

Merk: I filen colored_grid.py skal du ikke importere noe, og du skal heller ikke kalle på display-funksjonen. For å teste koden, opprett i stedet en separat fil colored_grid_test.py i samme mappe som colored_grid.py og kopier inn koden under. Når du kjører colored_grid_test.py, skal det tegnes tre rutenett på skjermen som vist under:

# colored_grid_test.py
from uib_inf100_graphics.simple import canvas, display
from colored_grid import draw_grid

def main():
    # Et 4x2 rutenett med farger
    draw_grid(canvas, 40, 100, 120, 180, [
            ['red', 'darkred'],
            ['yellow', 'orange'],
            ['white', ''], # den tomme strengen '' gir gjennomsiktig farge
            ['cyan', 'blue'],
        ]
    )

    # Et sjakkbrett
    draw_grid(canvas, 170, 30, 370, 250, [
            ['white', 'black'] * 4,
            ['black', 'white'] * 4,
        ] * 4
    )

    # En 2D-liste med kun én rad
    draw_grid(canvas, 50, 310, 350, 370, [
        ['#00c', '#01c', '#02c', '#03c', '#04c', '#05c', '#06c', '#07c',
        '#08c', '#09c', '#0ac', '#0bc', '#0cc', '#0dc', '#0ec', '#0fc']
    ])

    display(canvas)

if __name__ == '__main__':
    main()

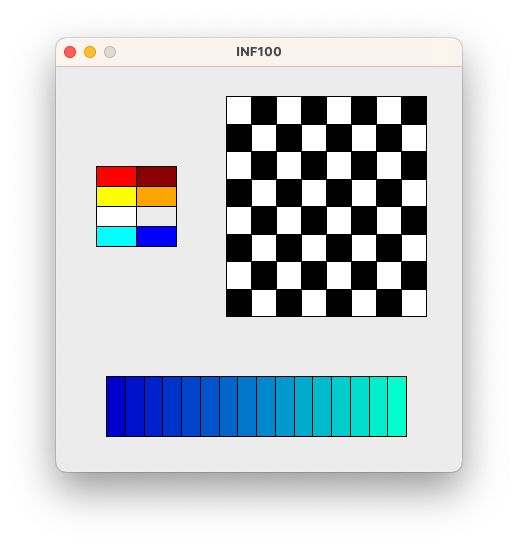
PS: I denne oppgaven skal du ikke fjerne outline når du tegner rektangler.

Ordspill

Denne oppgaven består av to deler. Skriv funksjoner til begge deloppgaver (A-B) i én felles fil, word_games.py.

I denne oppgaven skal vi skrive et hjelpemiddel for deg som ønsker å bli bedre i ordspill som Scrabble og Wordfeud. Det er selvfølgelig ikke lov å bruke dette for å jukse når man spiller på ordentlig, men det er lov å bruke det som et hjelpemiddel når man øver seg.

I spill som Scrabble og Wordfeud har hver spiller en bunke med brikker, som hver har én bokstav på seg. Poenget er å kombinere brikkene slik at de former et lovlig ord.

Del A

Opprett en funksjon can_be_made_of_letters(word, letters) som tar inn en streng word og en streng letters som parametre. Funksjonen skal returere True hvis strengen word kan lages med bokstavesamlingen letters, og False hvis ikke.

Her er en testfunksjon du kan bruke for testing:

def test_can_be_made_of_letters():
    print('Tester can_be_made_of_letters... ', end='')
    assert can_be_made_of_letters('emoji', 'abcdefghijklmno') is True
    assert can_be_made_of_letters('smilefjes', 'abcdefghijklmnopqrs') is False
    assert can_be_made_of_letters('smilefjes', 'abcdeeefhijlmnopsss') is True
    assert can_be_made_of_letters('lese', 'esel') is True
    print('OK')

# # Ekstra tester for mer avansert variant, med wildcard * i bokstavene
# def test_can_be_made_of_letters_wildcard():
#     print('Tester can_be_made_of_letters_wildcard... ', end='')
#     assert can_be_made_of_letters('lese', 'ese*') is True
#     assert can_be_made_of_letters('lese', 'esxz*') is False
#     assert can_be_made_of_letters('smilefjes', 's*i*e*j*s') is True
#     assert can_be_made_of_letters('smilefjes', 's*i*e*j*z') is False
#     print('OK')

Del B

Opprett en funksjon possible_words(wordlist, letters) som tar inn en liste med strenger wordlist og en streng letters som parametre. Funksjonen skal retunere en liste med alle ord fra wordlist som kan lages med bokstavene i letters. Ordene skal være i samme rekkefølge som i wordlist.

Her er en testfunksjon du kan bruke for testing:

def test_possible_words():
    print('Tester possible_words... ', end='')
    hundsk =['tur', 'mat', 'kos', 'hent', 'sitt', 'dekk', 'voff']
    kattsk =['kos', 'mat', 'pus', 'mus', 'purr', 'mjau', 'hiss']
    assert(['kos', 'sitt'] == possible_words(hundsk, 'fikmopsttuv'))
    assert(['kos', 'pus', 'mus'] == possible_words(kattsk, 'fikmopsttuv'))
    print('OK')

# # Ekstra tester for mer avansert variant, med wildcard * i bokstavene
# def test_possible_words_wildcard():
#     print('Tester possible_words_wildcard... ', end='')
#     hundsk =['tur', 'mat', 'kos', 'hent', 'sitt', 'dekk', 'voff']
#     kattsk =['kos', 'mat', 'pus', 'mus', 'purr', 'mjau', 'hiss']
#     assert ['tur', 'mat', 'kos', 'sitt'] == possible_words(hundsk, 'ikmopstu*')
#     assert ['kos', 'mat', 'pus', 'mus'] == possible_words(kattsk, 'ikmopstu*')
#     print('OK')

Komprimering

Denne oppgaven består av to deler. Skriv funksjoner til begge deloppgaver (A-B) i én felles fil, runlength_encoding.py.

En fil består av en sekvens av 1’ere og 0’ere. Noen filformater har i praksis veldig lange sekvenser med kun 1’ere eller kun 0’ere. For eksempel: en sensor i et alarmsystem gir 1 som output når en dør er åpen, og 0 som output når en dør er lukket; sensoren blir avlest 1 gang i sekundet, og disse data’ene blir lagret som en sekvens av 0’ere og 1’ere i en fil. Et annet eksempel på slike filer er bilder med store hvite eller svarte felter.

For å komprimere slike filer, kan vi omgjøre måten vi skriver filen på til å bestå av en sekvens heltall som forteller vekselvis hvor mange 0’ere og 1’ere som kommer etter hverandre. Det første tallet i komprimeringen forteller hvor mange 0’er det er i begynnelsen. Dette tallet kan være 0 dersom binærtallet begynner med 1. Alle andre tall i komprimeringen vil være positive. Du kan lese mer om denne typen komprimering på Wikipedia.

For enkelhets skyld gjør vi denne oppgaven med strenger og lister og ikke direkte med 1’ere og 0’ere lagret i minnet.

Del A

Opprett en funksjon compress(raw_binary) som tar inn en streng raw_binary bestående av 0’ere og 1’ere. Funksjonen skal retunerer en liste som representerer sekvensen i komprimert form (tall skilles med mellomrom).

Test deg selv:

def test_compress():
    print('Tester compress... ', end='')
    assert([2, 3, 4, 4] == compress('0011100001111'))
    assert([0, 2, 1, 8, 1] == compress('110111111110'))
    assert([4] == compress('0000'))
    print('OK')

Del B

Opprett en funksjon decompress(compressed_binary) som tar inn en liste compressed_binary beståenden av heltall som representerer en komprimert sekvens av 0’ere og 1’ere. La funksjonen returnere den ukomprimerte sekvensen av 0’ere og 1’ere.

Her er en testfunksjon du kan bruke for testing:

def test_decompress():
    print('Tester decompress... ', end='')
    assert('0011100001111' == decompress([2, 3, 4, 4]))
    assert('110111111110' == decompress([0, 2, 1, 8, 1]))
    assert('0000' == decompress([4]))
    print('OK')

Levende labyrint

Du jobber for et selskap som har utviklet en «levende» labyrint. Denne labyrinten er så vanskelig at den kan rotere seg selv for å skape nye veier og utfordringer for besøkende. Du har fått i oppgave å implementere en funksjon som roterer labyrinten.

I en fil labyrinth.py skriv en ikke-destruktiv funksjon rotate(grid, clockwise) som returnerer en 90-grader rotert versjon av grid. grid er en 2D-liste der hver av de indre listene har like mange elementer, og som derfor representerer en matrise. Det kan være at antall rader er forskjellig fra antall kolonner, det vil si at den ikke nødvendigvis er kvadratisk. Rotasjonen skal utføres med klokken hvis clockwise er True, og mot klokken hvis clockwise er False. Studer testene linket til under for å se hvordan rotasjonen skal utføres.

Siden testene tar mye plass, kan vi ha dem i en egen fil labyrinth_test.py. Hvis du vil kjøre testene når du kjører labyrinth.py, kan du legge til disse linjene i slutten av filen samtidig som du har lastet ned labyrinth_test.py i samme mappe.

if __name__ == '__main__':
    import labyrinth_test
    labyrinth_test.run_all()