Lab3
Kursnotater for tema som er nye i denne laben:
- En lab er en samling med én eller flere oppgaver.
- Hver lab kan gi opp til 25 poeng.
- Dersom du består alle oppgavene i hovedfeltet, får du 20 poeng. Alt eller ingenting.
- De resterende 5 poengene kan du få ved å gjøre oppgaver fra ekstrafeltet.
- Alle oppgaver rettes automatisk. Hvis du ikke består de automatiske testene, får du ikke poeng.
- De automatiske testene for grafikk-oppgaver sjekker bare at programmet ditt faktisk kjører, og så laster den opp bildet du lager i galleriet – den sjekker ikke om du faktisk har løst riktig oppgave. Vi gjør derfor en rask manuell sjekk på de grafiske oppgavene.
- Vi vil trekke poeng manuelt dersom vi oppdager at oppgaven åpenbart ikke er løst, eller man forsøker å trikse seg gjennom de automatiske testene.
- Hver lab kan leveres så mange ganger du vil; det er siste innlevering som teller. Du kan umiddelbart se resultatene på de automatiske testene og hvor mange poeng du har fått etter hver innlevering.
Hver lab utgjør 2.5% av den endelige karakteren din i emnet. Du må få til sammen 100 poeng eller mer på labene for å kunne ta eksamen.
Det er veldig viktig at du siterer alle kilder og eventuelle samarbeid. Se mitt.uib for mer informasjon om vår policy på plagiat og samarbeid.
Det er lurt å levere inn mange ganger underveis. Du får umiddelbart en automatisk tilbakemelding på oppgavene, og du kan prøve igjen hvis noe ikke virker.
Innlevering av lab’er foregår via verktøyet Codegrade som du kommer til via mitt.uib.
- Gå til «Oppgåver» i menyen til venstre
- Klikk deg videre til CodeGrade ved å klikke på «Last lab i eit nytt vindauge»
- Last opp filene du har laget for lab’en og trykk på «Submit.»
Fremdeles problemer? Se (merk at videoen er litt gammel, så det kan være noen små forskjeller i hvordan det ser ut nå.)
Ser du ikke knappen du skal trykke på i mitt.uib?
- Dobbeltsjekk at du er innlogget på mitt.uib.
- Prøv å laste siden i nettleseren på nytt.
- Prøv en «force refresh» (F5 eller Ctrl+F5 eller Ctrl+Shift+F5 eller Ctrl+Shift+R eller Command+R eller Command+Shift+R avhengig av nettleser og operativsystem).
- Prøv å tøm cache i nettleseren din (se refreshyourcache.com for hvordan du gjør dette) og prøv på nytt.
- Prøv en annen nettleser.
Tallrekke
Del A: Tallrekke med for-løkke
I en fil sequence.py, skriv en funksjon sequence_for() som tar inn et heltall n og bruker en for-løkke til å sette sammen en string av alle tall fra 0 til og med n med mellomrom mellom seg. Du kan anta at n er et positivt heltall.
Funksjonen range er veldig nyttig for å jobbe med tallrekker!
NB: Vi forventer at det er et mellomrom også på slutten av strengen som returneres.
Du kan begynne fra denne koden:
def sequence_for(n):
... # Din kode her
# Initialiser en tom streng
# For hvert tall i rekken fra 0 til og med n:
# Legg til tallet i strengen med mellomrom
# Returner streng
Her er tester du kan sette inn på slutten av filen for å teste funksjonen:
print("Tester sequence_for... ", end="")
assert "0 1 2 3 4 5 " == sequence_for(5)
assert "0 1 2 3 4 5 6 7 8 9 10 " == sequence_for(10)
assert "0 " == sequence_for(0)
print("OK")
Husk at range ikke inkluderer det siste tallet i rekken. For eksempel vil ikke range(5) inkludere tallet 5, men vil inkludere tallene fra 0 til og med 4.
Derfor trenger du å gi n+1 som argument til range for å få den til å inkludere n.
Del B: Tallrekke med while-løkke
I samme fil, skriv en funksjon sequence_while() som gjør det samme som over, men bruker i stedet en while løkke. Du kan begynne fra denne koden:
def sequence_while(n):
... # Din kode her
# Initialiser en tom streng
# Initialiser en variabel i til 0
# Så lenge i er mindre enn eller lik n:
# Legg til tallet i strengen med mellomrom
# Øk i med 1
# Returner streng
Her er tester til denne funksjonen som du kan sette under testene for del A:
print("Tester sequence_while... ", end="")
assert "0 1 2 3 4 5 " == sequence_while(5)
assert "0 1 2 3 4 5 6 7 8 9 10 " == sequence_while(10)
assert "0 " == sequence_while(0)
print("OK")
Tell x'er
I en fil count_xs.py, skriv en funksjon count_xs(s) som tar inn en streng s og returnerer antall x’er i strengen. Du kan anta at s kun inneholder små bokstaver.
Du kan begynne fra denne koden:
def count_xs(s):
... # Din kode her
# initialiser en variabel x_count til 0
# for hvert tegn i strengen:
# hvis tegnet er en x:
# øk x_count med 1
# returner x_count
Test koden din ved å legge til disse linjene nederst i filen:
print('Tester count_xs... ', end='')
assert 0 == count_xs('foo bar hei')
assert 1 == count_xs('x')
assert 4 == count_xs('xxCoolDragonSlayer99xx')
print('OK')
Den mest naturlige løsningen er å bruke en for-løkke fordi vi på forhånd vet hvor mange ganger vi skal gjenta løkken (like mange ganger som det er tegn i strengen):
def count_xs(s):
x_count = 0
for tegn in s:
if tegn == 'x':
x_count += 1
return x_count
Det er også mulig å løse oppgaven med en while-løkke, men det er litt mer knotete:
def count_xs(s):
x_count = 0
i = 0
while i < len(s):
if s[i] == 'x':
x_count += 1
i += 1
return x_count
Hold kjeft
Forberedelser: Repeter hvordan du beskjerer en streng: Beskjæring av strenger
I denne oppgaven skal vi skrive en funksjon som avbryter en setning. I en fil silence.py, lag en funksjon silence(). Denne funksjonen tar inn 2 parametere: sentence og n. Parameteren sentence er en streng, og n er et heltall større eller lik 0.
Hvis n er 0, skal funksjonen returnere sentence uendret. Hvis n er større eller lik lengden av sentence, skal funksjonen returnere en tom streng. Ellers skal funksjonen returnere en ny streng som er den opprinnelige strengen uten sine siste n tegn, pluss et - tegn.
Du kan starte fra denne koden:
def silence(sentence, n):
... # din kode her
Her er kode du kan legge til på slutten av filen som tester funksjonen din:
print("Tester silence... ", end="")
assert "Hei på deg!" == silence("Hei på deg!", 0)
assert "Hva skje-" == silence("Hva skjer?", 2)
assert "" == silence("Em.....", 7)
assert "Kan du slutte å avbryte-" == silence("Kan du slutte å avbryte meg?", 5)
assert ".-" == silence("...", 2)
print("OK")
Forelesning
Torstein vil vite hvor mange som har kommet på forelesning, og ønsker at noen skal telle det for han. Du har fått denne oppgaven og tenker å skrive et program som kan hjelpe deg å telle. Programmet ditt skal be brukeren om å oppgi hvor mange som nettopp kom inn døren, og så skal programmet legge dette til en total som skrives ut. Programmet skal fortsette å be om tall helt til brukeren skriver 0. Du kan anta at brukeren alltid skriver inn et heltall.
I filen lecture.py, skriv kode som gjør følgende:
- Lag en variabel
num_of_studentsog sett den til 0. - Lag en variabel
just_arrivedog sett den til 1. Dette tallet vil overskrives i løkken uansett, men må begynne som et tall større enn 0 - Lag en while-løkke som kjører så lenge
just_arrivedikke er lik 0. - Inne i løkken:
- Be brukeren om hvor mange som nettopp kom inn døren og lagre dette i variabelen
just_arrived. - Legg
just_arrivedtilnum_of_students. - Print hvor mange studenter som er kommet til nå.
- Be brukeren om hvor mange som nettopp kom inn døren og lagre dette i variabelen
break brukes for å avslutte en løkke. I denne oppgaven trenger vi ikke å bruke break fordi vi har en betingelse i løkken som sier at løkken skal skal fortsett kun hvis just_arrived er større enn 0. Når brukeren har skrevet inn 0 vil dette lagres i just_arrived, og løkkens betingelse vil ikke lenger være sann. Da vil løkken avsluttes.
Eksempelkjøring:
Hvor mange kom inn døren? 2
Det har kommet 2 studenter på forelesning.
Hvor mange kom inn døren? 3
Det har kommet 5 studenter på forelesning.
Hvor mange kom inn døren? -1
Det har kommet 4 studenter på forelesning.
Hvor mange kom inn døren? 0
Det har kommet 4 studenter på forelesning.
Smiley
I filen smiley.py ligger det en funksjon for å tegne et smilefjes. Last ned filen (vi trenger ikke endre på den for denne oppgaven, men les litt i den og forstå hva den gjør).
I tillegg kan du opprette filen smiley_grid.py i samme mappe. Begynn med å kopiere inn dette programmet:
| |
Når du kjører filen smiley_grid.py skal du se tre smilefjes delvis oppå hverandre.
Del A
Akkurat nå ligger smilefjesene oppå hverandre. Det hadde vært bedre om det var nok plass slik at smilefjesene ikke kommer oppå hverandre, men i stedet ligger inntil hverandre. Endre x -verdiene i listen på linje 5 slik at at smilefjesene ikke kommer oppå hverandre, men ligger helt inntil hverandre.
Del B
Vi ønsker å kunne enkelt justere hvor store smilefjesene er.
- Legg til
sizesom en parameter i draw_smiley_line -funksjonen. - Benytt size som argument når du gjør kallet til draw_smiley -funksjonen på linje 6.
- I funksjonskallet på linje 10, benytt 60 som et argument for size
Når du kjører programmet nå, skal det se slik ut:
Del C
Å nei! Smiley’ene ligger ikke inntil hverandre lengre! Vi må visst regne ut x-posisjonene basert på størrelsen.
- Uten å fjerne for-løkken: endre verdiene i listen av x-verdier slik de regnes ut på bakgrunn av størrelsen i stedet for å være helt faste verdier. Første x-verdi er 0, andre x-verdi er forskjøvet med like mye som størrelsen og så videre.
[0 * size, 1 * size, 2 * size]
Når du er ferdig skal funksjonkall med ulike verdier for størrelsen gi rader med smilefjes som ligger kant-i-kant uansett. Illustrasjonen under viser kjøringer av programmet der det eneste som er endret er størrelsesverdien vi gir som argument på linje 10.
Del D
Vi ønsker nå justere hvor mange smilefjes vi skal tegne.
- Legg til
nsom et andre parameter i draw_smiley_line -funksjonen slik at parametrene nå er både størrelse og antall. - I stedet for at for-løkken går over en fast liste med verdier, la den gå gjennom et range-objekt
range(n). Antall iterasjoner løkken utfører blir da bestemt avn. - Endre navnet på iteranden fra
xtili, siden iteranden nå ikke lengre representerer en x-verdi, men snarere en «indeks» som forteller hvilken iterasjon løkken har kommet til. - På en egen linje inne i løkken, opprett variabelen
xog regn ut en passende verdi for den. - I funksjonskallet til draw_smiley_line må du legge til et argument for antall fjes som skal tegnes, for eksempel 4.
x = i * size
Når du er ferdig skal funksjonskall med ulike verdier for n tegne en rad med n smilefjes som ligger kant-i-kant. Illustrasjonen under viser kjøringer av programmet der det eneste som er endret er argumentet for n (viser verdiene 0, 1, 2, 3, 4, 5).
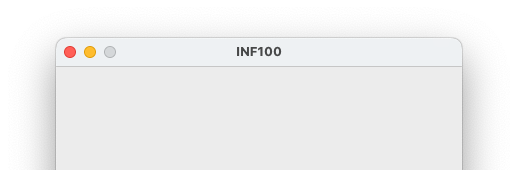
Del E
Vi ønsker nå å justere hvor smilefjesene tegnes på y-aksen
- Legg til
ysom den første parameteren i draw_smiley_line -funksjonen, slik at parametrene nå er(y, size, n). - Benytt denne parameteren når du kaller på draw_smiley
Når du er ferdig, kan du bytte ut hele if __name__ == '__main__' -blokken i programmet ditt med denne:
if __name__ == '__main__':
from uib_inf100_graphics.simple import canvas, display
draw_smiley_line(0, 60, 5)
draw_smiley_line(60, 100, 3)
draw_smiley_line(160, 60, 5)
display(canvas)
Kjør programmet ditt og se følgende bilde:
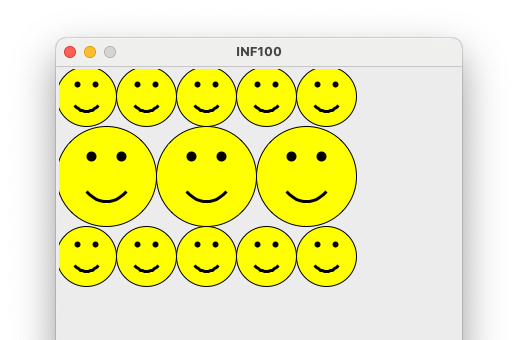
Del F
I filen smiley_grid.py, opprett en funksjon draw_smiley_grid med parametre size og n. Funksjonen skal tegne et rutenett med smilefjes, der size er størrelsen til ett smilefjes, og n er antall smiljefjes i begge retninger.
Når du er ferdig, kan du bytte ut hele if __name__ == '__main__' -blokken i programmet ditt med denne:
if __name__ == '__main__':
from uib_inf100_graphics.simple import canvas, display
draw_smiley_grid(70, 5)
display(canvas)
Om du har gjort alt riktig kan du kjøre programmet ditt og se følgende bilde:
Bruk en for-løkke for å kalle på draw_smiley_line
ngangerRegn ut en egnet verdi for
yi hver iterasjon av løkken (dette ligner veldig 😉 på hvordan du regnet ut x)
Vokaler
I filen vowels.py, skriv en funksjon vowels() som tar inn en streng text og returnerer hvor mange vokaler som er i text. I denne oppgaven anser vi kun bokstavene «a», «e», «i», «o», «u» som vokaler. Husk å telle med både store og små bokstaver!
Her er kode du kan legge på slutten av filen for å teste funksjonen din:
print("Tester vowels... ", end="")
assert 5 == vowels("Pingu in the city")
assert 9 == vowels("Frieren: Beyond Journey's End")
assert 3 == vowels("Programming")
assert 0 == vowels("Hmm")
print("OK")
For å telle både små og store bokstaver kan du bruke .lower() for å endre alle store bokstavene til små. For eksempel, koden nedenfor skriver ut dette er en streng:
streng = "Dette er EN Streng"
streng = streng.lower()
print(streng)
Chatbot
I denne oppgaven skal du lage en veldig primitiv chatbot. Chatboten skal altså bare kunne si tre ting: «Hi! Do you want to talk to me?», «That’s cool!», eller «All right, bye!».
I filen chatbot.py, skriv kode som gjør følgende:
- Ber brukeren for input med teksten, «Hi! Do you want to talk to me?».
- Om brukeren skriver inn, «no» skal programmet skrive ut, «All right, bye!» og avslutte å kjøre.
- Om brukeren skriver in noe annet enn «no», skal programmet skrive ut «That’s cool!», og siden be om input fra brukeren igjen med teksten, «Hi! Do you want to talk to me?»
Eksempelkjøring:
Hi! Do you want to talk to me?
yes
That's cool!
Hi! Do you want to talk to me?
egentlig ikke
That's cool!
Hi! Do you want to talk to me?
no
All right, bye!
Denne oppgaven kan løses på flere måter, men siden vi ikke vet hvor mange ganger løkken skal kjøres på forhånd, må vi i alle tilfeller bruke en while-løkke.
Alternativ A: Du kan benytte en while True -løkke, og så benytte break dersom brukeren svarer no.
En iterasjon av den innerste løkken er ansvarlig for å skrive ut ett tall, nemlig produktet av iterandene (løkke-variablene) fra de to løkkene.
Alternativ B: Du kan opprette en variabel answer = "" før while -løkken starter, og la betingelsen for while-løkken være answer != “no”.
Største faktor
En faktor i et positivt heltall \(x\) er et annet og mindre heltall \(y\) slik at \(\frac{x}{y}\) også er et heltall. Dersom den største faktoren i \(x\) er 1, sier vi at \(x\) er et primtall.
I denne oppgaven ønsker vi å finne den største faktoren i et gitt tall. I filen find_factor.py skriv en funksjon largest_factor_of med en parameter x, tallet vi ønsker å finne den største faktoren for. Funksjonen skal returnere den største faktoren i x.
For å teste funksjonen
def test_largest_factor_of():
print('Testing largest_factor_of... ', end='')
assert 3 == largest_factor_of(6)
assert 1 == largest_factor_of(7)
assert 4 == largest_factor_of(8)
print('OK')
if __name__ == '__main__':
test_largest_factor_of()
For å sjekke om y er en faktor i x, kan vi benytte modulo-operasjonen % for å se hva restverdien blir etter en heltallsdivisjon. Om denne er 0 betyr det at f er en faktor i x.
For å finne den største faktoren kan vi prøve alle mulige faktorer (alle heltall mellom 1 og x) i en løkke og ta vare på den største av dem.
Oppdelt linjestykke
Del A: Finn endepunkter for et enkelt segment
Et linjestykke langs x-aksen begynner i et punkt \(x_{\text{lo}}\) og slutter i et punkt \(x_{\text{hi}}\). Vi ønsker å klippe opp linjestykket i \(n\) like store biter. Til slutt vil vi vite hvor bit nummer \(i\) begynner og slutter.
For eksempel, hvis
- \(x_{\text{lo}} = 50\)
- \(x_{\text{hi}} = 150\)
- \(n = 4\)
- \(i = 1\)
da er svaret vi leter etter \((75, 100)\). Se illustrasjon:
I filen split_line.py lag en funksjon get_endpoints. Denne funksjonen skal ha fire parametere: i, n, x_lo og x_hi. Parametrene x_lo og x_hi er flyttall og definerer linjestykket som nevnt ovenfor. Parametrene i og n er begge heltall. Funksjonen skal returnere start- og sluttpunktet for segmentet med indeks i når vi deler hele linjen i n like store deler. For eksempel: get_endpoints(1, 4, 50.0, 150.0) skal returnere 75.0, 100.0, og get_endpoints(3, 4, 50.0, 150.0) skal returnere 125.0, 150.0.
Legg merke til at lengden til det opprinnelige linjestykkebit er $$\ell_{\text{tot}} = x_{\text{hi}}-x_{\text{lo}}$$
Lengden til en utklippet bit blir da $$\ell_{\text{bit}} = \frac{\ell_{\text{tot}}}{n}$$
Observer også at utklippet bit nummer \(i\) begynner i $$x_{i\text{lo}} = x_{\text{lo}} + i \cdot \ell_{\text{bit}}$$ og slutter i $$x_{i\text{hi}} = x_{i\text{lo}} + \ell_{\text{bit}}$$
PS: funksjoner kan returnere flere verdier. Følgende eksempel viser hvordan:
def foo(bar):
a = 2 * bar
b = 3 * bar
return a, b
x, y = foo(5)
print(x) # 10
print(y) # 15
Test deg selv:
def almost_equals(a, b):
return abs(a - b) < 0.0000000001
print('Testing get_endpoints... ', end='')
start, end = get_endpoints(1, 4, 50.0, 150.0)
assert almost_equals(75, start)
assert almost_equals(100, end)
start, end = get_endpoints(3, 4, 50.0, 150.0)
assert almost_equals(125, start)
assert almost_equals(150, end)
start, end = get_endpoints(0, 3, -30, 60)
assert almost_equals(-30, start)
assert almost_equals(0, end)
print('OK')
Del B: Lag et interaktivt program
I samme fil (split_line.py) utvid koden med en if __name__ == '__main__' -blokk slik at når du kjører programmet så blir brukeren bedt om å:
- oppgi \(x_{\text{lo}}\)
- oppgi \(x_{\text{hi}}\)
- oppgi tallet \(n\); antall biter linjestykket skal deles opp i.
Deretter skriver programmet ditt ut n linjer, der hver linje består av to tall som representerer et linjestykke. Benytt funksjonen fra del A for å finne punktene (du skal altså ikke gjøre alt på nytt, men i stedet kalle på funksjonen vi allerede har skrevet).
Eksempelkøringer skal se sånn ut:
x_lo = 1.0
x_hi = 7.0
n = 3
1.0 3.0
3.0 5.0
5.0 7.0
x_lo = 0.0
x_hi = 1.0
n = 4
0.0 0.25
0.25 0.5
0.5 0.75
0.75 1.0
I denne oppgaven vet du allerede før løkken starter hvor mange iterasjoner løkken skal ha (nemlig n). Derfor bør du velge en for-løkke, og ikke en while-løkke.
Fargetog
I denne oppgaven skal vi lage en funksjon som tegner et tog med fargede vogner på et uib_inf100_graphics.simple canvas.
PS: Vi er klar over at resultatet ikke egentlig ligner på et tog, men det er gøyere å kalle det et tog enn en rekke med fargede rektangler.
Kun oppgaven under Del A er obligatorisk, men vi anbefaler at du prøver resten også
Forberedelser: Repeter hvordan du går gjennom alle elementene i en samling med strenger: For-løkker over range
Når du leverer denne oppgaven på CodeGrade, vil et skjermbilde av programmet ditt automatisk lastes opp til galleriet, hvor du også kan se dine medstudenter sine besvarelser.
Del A: Tegn et tog med fargede vogner
Vi begynner med den enkleste versjonen av denne oppgaven.
I filen color_train.py, lag en funksjon color_train_A(). Denne funksjonen tar inn 4 parametere: canvas, x, y, colors. Funksjonen skal tegne fargede ruter (eller vogner) med en fast størrelse på 15 x 10px (bredde x høyde) etter hverdandre på canvaset. Rekken av vogner skal starte på \((x, y)\) og gå fra venstre til høyre. Fargene er gitt i listen colors.
For eksempel, hvis rekken av farger er ["white", "black", "white"] så skal første vognen (fra venstre) være hvit, andre vognen skal være svart og tredje vognen hvit.
Merk: Du skal ikke kalle på display-funksjonen i samme fil som du skriver funksjonene. For å teste koden, opprett en separat fil color_train_test.py i samme mappe som color_train.py og kopier inn koden du finner under (i Testing-boksen):
from uib_inf100_graphics.simple import canvas, display
from color_train import color_train_A#, color_train_B, color_train_C
colors1 = ['violet', 'indigo', 'blue', 'green', 'yellow', 'orange', 'red']
colors2 = ['black', 'white', 'black', 'white', 'black', 'white']
colors3 = ['#800080', '#8B008B', '#9400D3',
'#9932CC', '#8A2BE2', '#9370DB',
'#7B68EE', '#6A5ACD', '#483D8B',
'#0000FF', '#0000CD', '#00008B',
'#000080', '#191970', '#00008B']
color_train_A(canvas, 10, 10, colors1)
color_train_A(canvas, 10, 20, colors2)
color_train_A(canvas, 10, 40, colors3)
display(canvas)
Når du kjører color_train_test.py, skal det tegnes 3 tog på skjermen som vist under:
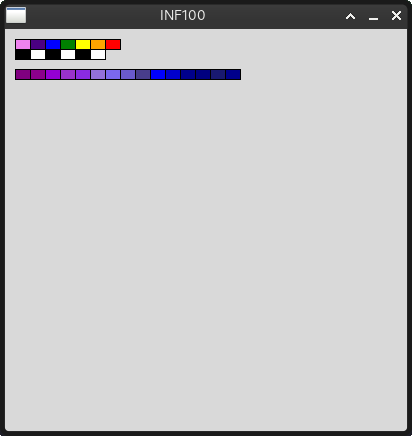
Del B: Tegn et fargetog med oppgitt høyde og bredde
I denne delen skal vi lage en alternativ funksjon som tegner et tog med en gitt høyde og bredde.
I color_train.py, skriv en funksjon color_train_B() som tar inn 6 parametere: canvas, x, y, width, height og colors. Som color_train_A() skal funksjonen tegne fargede rektangler etter hverandre, men nå skal den totale bredden på toget være width og høyden skal være height. Det betyr at du må regne ut bredden til hver enkelt vogn fra dette.
For å teste koden, i color_train_test.py (fra Del A) legg til disse funksjonskallene rett før display(canvas):
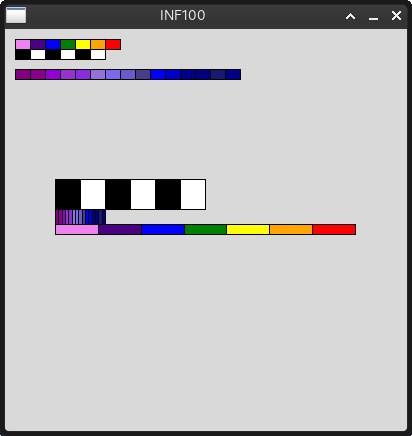
color_train_B(canvas, 50, 195, 300, 10, colors1)
color_train_B(canvas, 50, 150, 150, 30, colors2)
color_train_B(canvas, 50, 180, 50, 15, colors3)
Pass på at du flytter på kommentaren i toppen av test-filen slik at bare color_train_C er kommentert ut. Den må forbli kommentert ut fram til du gjør Del C.
Når du kjører color_train_test.py, skal det tegnes 3 nye tog på skjermen som vist under:
Del C: Tegn et fargetog bare med koordinater
I denne delen skal vi lage enda en ny funksjon color_train_C() som tar inn 6 parametere:
canvas, x1, y1, x2, y2 og colors. Funksjonen skal gjøre det samme som i B, men tar nå utgangspunkt i to punkter: \((x_1, y_1)\) og \((x_2, y_2)\). Disse to punktene skal være øvre venstre hjørne og nedre høyre hjørne til det ferdige toget.
For å teste koden, i color_train_test.py (fra Del A) legg til disse funksjonskallene rett før display(canvas):
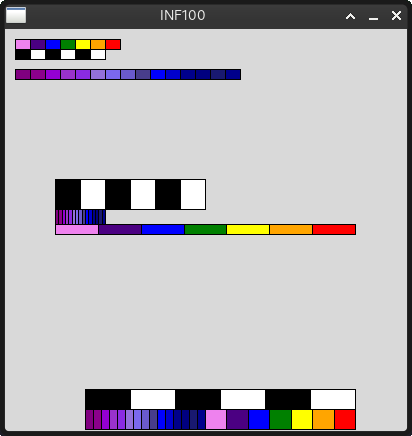
color_train_C(canvas, 200, 380, 350, 400, colors1)
color_train_C(canvas, 80, 360, 350, 380, colors2)
color_train_C(canvas, 80, 380, 200, 400, colors3)
Hvis du regner høyde og bredde fra punktene, kan du gjenbruke color_train_B() her.
Når du kjører color_train_test.py, skal det tegnes 3 nye tog på skjermen som vist under:
Sparing
Du er uteksaminert fra UiB og har nå en flott jobb! Du flytter til London og bestemmer deg for at du vil begynne å spare for å kjøpe hus. Siden boligprisene er svært høye i London, innser du at du må spare i flere år før du har råd til å skaffe deg egenkapital. Vi skal finne ut hvor lang tid det vil ta deg å spare nok egenkapital gitt følgende forutsetninger:
- Egenkapital er 0,25 (25%) av total kostnad.
- Beløpet du har spart så langt er null.
- Anta at sparingene dine tjener en årlig rente \(r = 0.04\) (4%).
I filen saving.py skriv en funksjon som tar inn tre tall som input:
- Årslønn.
- Prosentandel av lønnen som skal spares.
- Totalkostnaden for drømmeboligen.
Funnksjonen skal returnere hvor mange måneder det vil ta deg å spare opp nok egenkapital. Her kan du anta at det etter hver måned blir utbetalt \(r/12\) i renter av det som står på konto.
Her er kode du kan legge til på slutten av filen for å teste funksjonen din:
print("Tester saving... ", end="")
assert saving(500000, 20, 3000000) == 79
assert saving(900000, 10, 5000000) == 133
print("OK")
Befolkningsvekst
I denne oppgaven skal du skrive et program som beregner befolkningsvekst. Programmet skal lese inn tre tall. Først den opprinnelige størrelsen av en populasjon som et heltall, så den årlige veksten som flyttall, også antall år som skal beregnes som et heltall. For hvert år skal programmet skrive ut estimatet av de nye befolkningstørrelsen, rundet ned til nærmeste heltall. Til slutt skal programmet skrive ut totalveksten av startbefolkningen i prosent med to desimalers nøyaktighet (det er ikke nødvendig å skrive ut avsluttende nullere (trailing zeros), man kan med andre ord bruke round() funksjonen).
Kort oppsummert, i filen population_growth.py skriv et program som:
- Ber brukeren om nåværende befolkning, en spesifikk vekstrate og antall år som skal beregnes (se eksempelkøringene for nøyaktig ordlyd).
- Skriver ut én linje per år som beregnes, med antatt befolkning gitt oppgitt vekstrate.
- Skriver ut en linje på slutten som oppgir den totale veksten etter oppgitt antall år i prosent.
For å forenkle testingen, spesifiserer vi her at du alltid skal representere folkemengden som et heltall, selv i mellomregninger. Vi kan jo ikke bare ha et halvt menneske. For å få dette til kan du kalle
int()med det utregnede flyttalet som argument. I første eksempelet under er folkemengden etter 1 år: $$1000 + 1000 \times 0.0248 = 1024.8$$ Men vi runder ned til 1024. Det er også 1024 som brukes videre for å beregne neste år, altså: $$1024 + 1024 \times 0.0248 = 1049.4$$ og vi runder ned til 1049.
Eksempelkøringer:
Befolkning: 1000
Årlig vekstrate (i prosent): 2.48
Antall år: 5
Befolkningen etter 1 år er 1024
Befolkningen etter 2 år er 1049
Befolkningen etter 3 år er 1075
Befolkningen etter 4 år er 1101
Befolkningen etter 5 år er 1128
Total vekst etter 5 år er (i prosent) 12.8
Befolkning: 797510515
Årlig vekstrate (i prosent): 0.83
Antall år: 3
Befolkningen etter 1 år er 804129852
Befolkningen etter 2 år er 810804129
Befolkningen etter 3 år er 817533803
Total vekst etter 3 år er (i prosent) 2.51
Tegn π
Opprette en fil draw_pi.py og kopier inn dette programmet:
from uib_inf100_graphics.simple import canvas, display
import random
def draw_dot(canvas, x, y):
canvas.create_oval(x-5, y-5, x+5, y+5, fill='orange')
# Draw a circle in the window
canvas.create_oval(0, 0, 400, 400)
# Highlight a random point on 400x400 canvas
x = random.random() * 400
y = random.random() * 400
draw_dot(canvas, x, y)
display(canvas)
Kjør programmet et par ganger. Sjekk at programmet tegner en liten prikk et tilfeldig sted hver gang programmet kjøres, i tillegg til å tegne en stor sirkel med radius 200 og sentrum i punktet (200, 200).
Del A: tegn mange tilfeldige prikker
Endre koden slik at det ikke bare er én prikk som tegnes, men 1000 tilfeldige prikker. Når du er ferdig skal en kjøring av programmet se omtrent slik ut:
n = 1000
for _ in range(n):
# Kode for å generere ett tilfeldig punkt og tegne det legges her
...
Del B: fargelegg prikkene som er innenfor sirkelen
Endre programmet slik at prikkene som er innenfor sirkelen får en annen farge enn prikkene som er utenfor. Vi sier at en prikk er innenfor sirkelen dersom avstanden fra prikkens sentrum til sirkelens sentrum er mindre enn sirkelens radius, nemlig 200. Sirkelen har sentrum i punktet (200, 200). Når du er ferdig, skal en kjøring av programmet se omtrent slik ut:
- Legg til en parameter for farge i funksjonen som tegner en prikk.
- Bruk en if/else-setning for tegne prikken med enten den ene eller den andre fargen. Betingelsen er at avstanden til sirkelens sentrum (200, 200) er mindre enn 200.
- For å regne ut avstanden mellom to punkter: du kan gjenbruke funksjonen for å beregne avstand fra en tidligere lab, eller du kan regne det ut på nytt.
Del C: tell hvor mange prikker som er innenfor sirkelen
Endre programmet slik at du skriver ut en melding på skjermen som forteller hvor mange av prikkene som er innenfor sirkelen og hvor mange som er utenfor.
- Før løkken: opprett en tellevariabel med initiell verdi 0
- Inne i løkken: når betingelsen er oppfylt slik at det tilfeldige punktet er innenfor sirkelen, øk tellevariabelen med én.
- Etter løkken: tegn en firkant på toppen av bildet ditt. Oppå firkanten kan du skrive en streng.
# Eksempel som skriver ut tekst på toppen av en firkant
message = 'Carpe diem'
canvas.create_rectangle(100, 180, 300, 220, fill='white')
canvas.create_text(200, 200, text=message, fill='blue')
Del D: finn \(\pi\)
\(\pi\) er definert som en sirkels omkrets delt på sin diameter. Uten å vite nøyaktig hvilken verdi \(\pi\) har, kan matematikere bevise at denne verdien, om vi en vakker dag skulle få vite hva den er, kan brukes for å regne ut en sirkel sitt areal:
$$ A_{\bigcirc} = \pi \cdot r^2 $$
Den beste tilnærmingen vi har til \(\pi\) i skrivende stund inneholder over \(10^{12}\) siffer. I Python har vi en tilnærmingen gitt ved
math.pibegrenset til de første 15 siffrene. Det finnes andre moduler som gir oss en bedre tilnærming, men da må vi slutte å brukefloatog heller bruke en annen datatype som er i stand til å gi oss høyere presisjon.
Vi har i de forrige deloppgavene tegnet en sirkel med radius \(r = 200\) som befinner seg inne i et kvadratisk lerret med sidelengde \(s = 400\). Vi legger verdiene for r og s inn i formelene for areal av henholdsvis sirkler og kvadrat, og får følgende:
$$A_{\bigcirc} = \pi \cdot r^2 = \pi \cdot 200^2 = \pi \cdot 40\,000$$ $$A_{\square} = s^2 = 400^2 = 160\,000$$
Dersom vi velger et helt tilfeldig punkt inne i kvadratet, vil punktet med viss sannsynlighet \(p\) også havne inne i sirkelen. Fordi sirkelen er omsluttet av kvadratet på alle kanter, ser vi at \(p\) er gitt ved forholdet mellom arealet av sirkelen og kvadratet:
$$ p = \frac{A_{\bigcirc}}{A_{\square}} = \frac{\pi \cdot 40\,000}{160\,000} = \frac{\pi}{4}$$
Det følger at hvis vi klarer å finne ut hva \(p\) er for noe, trenger vi bare multiplisere tallet med 4 for å finne \(\pi\). Det leder oss til følgende algoritme:
- Gjett et tilfeldig punkt mellom (0, 0) og (400, 400)
- Sjekk om punktet er innenfor eller utenfor sirkelen
- Gjenta steg 1-2 tilstrekkelig mange ganger, og tell opp hvor ofte det tilfeldige tallet havnet inne i eller utenfor sirkelen. Da bli forholdet mellom antall treff i sirkel og totalt antall genererte punkter tilnærmet lik \(p\). La oss kalle tilnærmingen \(\hat{p}\). $$\frac{\text{antall prikker i sirkel}}{\text{antall prikker totalt}} = \hat{p} \approx p$$
- Gang opp \(\hat{p}\) med 4 for å finne en tilnærmet verdi for \(\pi\).
For å gjennomføre algoritmen, gjenstår det altså kun å regne ut \(\hat{p}\), multiplisere med fire og skrive ut estimatet på skjermen. Når du er ferdig, skal en kjøring av programmet se omtrent slik ut:
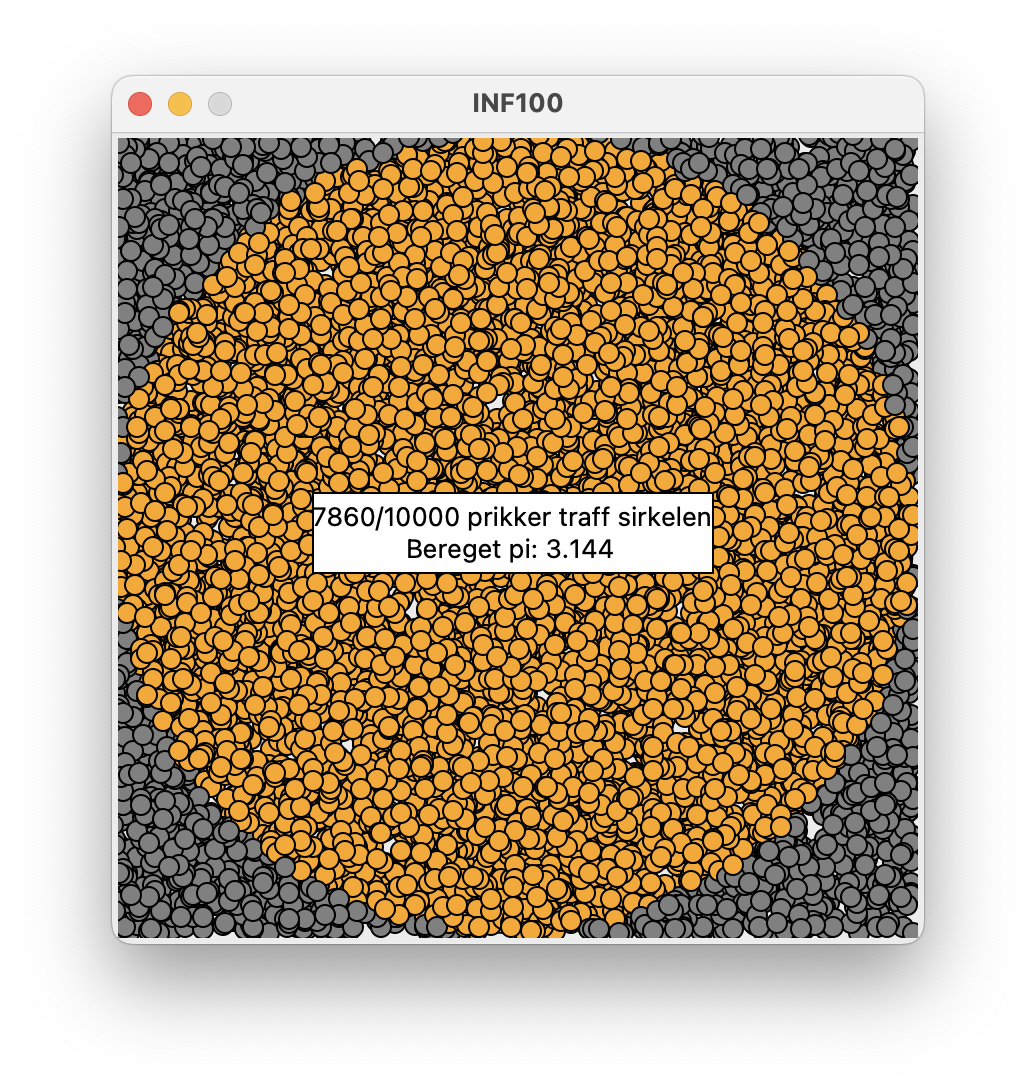
PS: For å få en bedre tilnærming av \(\pi\) kan du øke antall tilfeldige prikker, for eksempel er antallet prikker økt til \(10\,000\) i skjermbildet over. Når du leverer oppgaven på CodeGrade ber vi imidlertid om at du begrenser antall prikker til \(1\,000\) slik at maskinen ikke blir overbelastet.
Tverrsum
En tverrsum er summen av alle sifrene i et tall. For eksempel, tverrsummen av tallet 123 er 1 + 2 + 3 = 6.
Del A: Tverrsum
I filen cross_sum.py skriv en funksjon cross_sum som med en parameter x som tar inn et heltall og returnerer tverrsummen av tallet.
Du kan begynne fra denne koden:
def cross_sum(x):
... # din kode her
Her er tester du kan sette inn på slutten av filen for å teste funksjonen:
def test_cross_sum():
print('Tester cross_sum... ', end='')
assert 6 == cross_sum(123)
assert 7 == cross_sum(34)
assert 0 == cross_sum(0)
assert 1 == cross_sum(100)
print('OK')
if __name__ == '__main__':
test_cross_sum()
Del B: N-te tallet med tverrsum
I samme fil, skriv en funksjon nth_cross_sum med parametre n og x som tar inn heltall og som returnerer ut det n’te tallet med tverrsummen x.
Eksempel: det første tallet med tverrsum 7 er bare tallet 7, mens det andre tallet med tverrsum 7 er 16. Derfor skal programmet ditt skrive ut 7 på input n = 1 og x = 7, mens programmet skal ut 16 på input n = 2 og x = 7.
Her er kode du kan legge til på slutten av filen for å teste funksjonen din:
def test_nth_cross_sum():
print('Tester nth_cross_sum... ', end='')
assert nth_cross_sum(3, 7) == 25
assert nth_cross_sum(1, 10) == 19
assert nth_cross_sum(2, 10) == 28
assert nth_cross_sum(10, 2) == 2000
print('OK')
if __name__ == '__main__':
test_nth_cross_sum()
Du vet ikke før løkken starter hvor mange iterasjoner løkken skal ha. Derfor bør du velge en while-løkke, og ikke en for-løkke for å finne det n-te tallet med en gitt tverrsum.
Animasjon
Denne koden tegner en ball som blir sluppet fra en gitt høyde, 300 piksler over bunnen av skjermen.
from uib_inf100_graphics.simple import canvas, display
y_pos_px = 100
y_vel_px_s = 0
radius = 20
gravity_px_s2 = 100
time_delta_s = 0.1 # Som standard viser display et bilde i 0.1 sekunder
while True:
# La tiden gå
y_vel_px_s += gravity_px_s2 * time_delta_s
y_pos_px += y_vel_px_s * time_delta_s
# Tegne
canvas.create_oval(200 - radius, y_pos_px - radius,
200 + radius, y_pos_px + radius, fill="red")
display(canvas)
Akkurat nå forsvinner ballen ut av skjermen når den treffer bunnen. Din jobb er å endre legge til noen linjer i koden slik at ballen spretter opp igjen når den treffer bunnen av skjermen.
- Linjene du skal legge til passer bra å ha mellom ballen har blitt flyttet og ballen har blitt tegnet på nytt.
- Hvis ballen har falt ut av skjermen, da kan du endre fortegnet på farten til ballen.
- Hvilken betingelse skal du sjekke for å finne ut om ballen er utenfor skjermen?
I filen animation.py, skriv et program som lager en valgfri animasjon ved hjelp av rammmeverket uib_inf100_graphics.simple.
Når du leverer denne oppgaven på CodeGrade, vil et skjermbilde av programmet ditt automatisk lastes opp til galleriet, hvor du også kan se dine medstudenter sine besvarelser.