Lab2
Kursnotater for tema som er nye i denne laben:
Hale på grisen
Før du gjør denne oppgaven, må du installere grafikk-biblioteket vi benytter i emnet. Se instruksjoner i kursnotater om grafikk.
Det følgende programmet tegner en gris; men uheldigvis er halen plassert feil sted. Opprett en fil pigs_tail.py hvor du kopierer inn koden under, men endrer den slik at halen blir tegnet på riktig sted (omtrent som vist på bildet under).
from uib_inf100_graphics.simple import canvas, display
# Legs
canvas.create_rectangle(110, 230, 150, 300, fill="pink")
canvas.create_rectangle(300, 230, 340, 300, fill="pink")
canvas.create_rectangle(80, 260, 120, 330, fill="pink")
canvas.create_rectangle(280, 260, 320, 330, fill="pink")
# Ears
canvas.create_polygon(260, 70, 260, 30, 290, 60, fill="pink", outline="black")
canvas.create_polygon(310, 55, 330, 30, 340, 70, fill="pink", outline="black")
# Body
canvas.create_oval(50, 100, 350, 300, fill="pink")
# Head
canvas.create_oval(250, 50, 350, 150, fill="pink")
# Eyes
canvas.create_oval(280, 70, 295, 85, fill="black")
canvas.create_oval(320, 70, 335, 85, fill="black")
# Nose
canvas.create_oval(290, 100, 330, 130, fill="lightpink")
canvas.create_oval(295, 110, 305, 120, fill="black")
canvas.create_oval(315, 110, 325, 120, fill="black")
# Tail
canvas.create_line(200, 50, 150, 20, 100, 50)
display(canvas)
Eksempelløsning:

Du står fritt til å tegne en enda finere hale dersom du ønsker. Når du leverer denne oppgaven på CodeGrade, vil et skjermbilde av programmet ditt automatisk lastes opp til galleriet hvor du også kan se dine medstudenter sine besvarelser.
-
Halen tegnes på den linjen som begynner med
canvas.create_line. Denne funksjonen trekker en linje mellom to eller flere punkter (her: tre punkter). -
Tallene mellom parenteser angir koordinatene hvor linjen skal trekkes. Tallene kommer parvis x1, y1, x2, y2, x3, y3 og så videre. For eksempel betyr de to første tallene i utlevert kode (
200, 50) at linjen som trekkes starter i punktet (x1=200, y1=50). -
Husk: vinduet har størrelse 400x400.
-
Begynn med å endre kun det første punktet; flytt det slik at halen begynner ved grisen sin rumpestump.
-
Flytt deretter de andre to punktene, slik at du får en fin hale.
Suppe
Programmet under tegner én boks med suppe. Kopier det inn i filen soup.py.
from uib_inf100_graphics.simple import canvas, display
def draw_soup_can(canvas, x, y, bg_color, text_color):
canvas.create_rectangle(x, y+10, x+100, y+130, fill=bg_color)
canvas.create_oval(x, y, x+100, y+20, fill='gray')
canvas.create_oval(x, y+120, x+100, y+140, fill='gray')
canvas.create_text(x+50, y+50, text='SOUP',
fill=text_color, font=('Arial', 16, 'bold'))
draw_soup_can(canvas, 50, 30, 'red', 'yellow')
# TODO: make three more calls to draw_soup_can with different arguments
display(canvas)
Skriv tre nye linjer med kode hvor du kaller funksjonen draw_soup_can med andre argumenter, slik at du får tegnet fire bokser med suppe som vist her:

Marilyn
Dette programmet tegner en vakker kvinne fire ganger. Kopier det inn i filen marilyn.py.
from uib_inf100_graphics.simple import canvas, display
def draw_marilyn(canvas, x, y):
# Background
canvas.create_rectangle(x, y, x+100, y+100, fill='red', outline='')
# Face
canvas.create_oval(x+20, y+20, x+80, y+80, outline='yellow', width=2)
# Eyes
canvas.create_oval(x+35, y+40, x+45, y+50, fill='yellow', outline='')
canvas.create_oval(x+55, y+40, x+65, y+50, fill='yellow', outline='')
# Mouth
canvas.create_arc(x+35, y+50, x+65, y+70, start=180, extent=180,
fill='yellow', outline='')
# Drawing four faces
draw_marilyn(canvas, 50, 50)
draw_marilyn(canvas, 250, 50)
draw_marilyn(canvas, 50, 250)
draw_marilyn(canvas, 250, 250)
display(canvas)
For å gjøre tegningen litt mer interessant, endre draw_marilyn -funksjonen slik at den i tillegg til x og y også tar inn to nye parametre background_color og detail_color. Oppdater funksjonskroppen (kodelinjene inne i funksjonen) slik at den benytter disse fargene i stedet for hardkodete farger når den tegner
I de fire funksjonskallene som utfører tegningen, velg ulike farger etter eget ønske. Det endelige resultatet kan for eksempel se slik ut:
Paritet
I filen parity.py, skriv en funksjon parity(x) som har en parameter x, og som returnerer Partall hvis x er et partall og Oddetall hvis x er et oddetall. Du kan anta i funksjonen at x er et heltall med typen int.
def parity(x):
# Skriv koden din her
For å teste funksjonen din kan du legge til dette på slutten av filen:
print('Tester parity... ', end='')
assert 'Partall' == parity(0)
assert 'Oddetall' == parity(1)
assert 'Partall' == parity(42)
assert 'Oddetall' == parity(99)
print('OK')
-
Benytt modulo (
%) for å avgjøre om et tall er partall eller oddetall. Mer informasjon om modulo finner i kursnotatene om operatorer
Hundeår
Vanligvis sier man at et menneskeår tilsvarer 7 hundeår. Dette tar ikke hensyn til at hunder blir voksne når de er ca 2 år. Derfor kan det være bedre å regne begge de første 2 menneskeårene som 10.5 hundeår hver, og etter det regne hvert menneskeår som 4 hundeår.
I filen dog_years.py skal du opprette funksjonen human_to_dog_years med én parameter som representerer antall menneskeår. La funksjonen returnere hvor mange hundeår dette tilsvarer.
Test koden din (husk at du også må legge inn et funksjonskall til test-funksjonen for at testene faktisk skal kjøres):
def almost_equals(a, b):
return abs(a - b) < 0.00000001
def test_human_to_dog_years():
print('Tester human_to_dog_years... ', end='')
assert almost_equals(15.75, human_to_dog_years(1.5))
assert almost_equals(21.00, human_to_dog_years(2))
assert almost_equals(57.00, human_to_dog_years(11))
print('OK')
Grisete samarbeid
Teamet ditt med utviklere skal tegne en fin gris, og dere har fordelt arbeidet som følger:
- Ola tegner grisens hode med en funksjon
draw_headi filen pig_head.py. - Kari tegner grisens kropp med en funksjon
draw_bodyi filen pig_body.py. - Din jobb er å skrive hovedfilen pig_main.py som binder sammen tegningene og som faktisk tegner en gris når programmet kjører.
I denne oppgaven skal du ikke endre på filene pig_head.py eller pig_body.py, du skal bare laste dem ned.
Ola og Kari er ferdig med arbeidet sitt; last ned filene de har laget (høyreklikk på linkene og velg «lagre» eller lignende). Opprett deretter en fil pig_main.py som du legger i samme mappe som filene fra Ola og Kari.
- Øverst i pig_main.py, importer funksjonene draw_head og draw_body fra henholdsvis pig_head og pig_body -filene.
- Du må også importere canvas og display fra uib_inf100_graphics.simple slik du pleier. På slutten av filen må du kalle på display(canvas), slik vi også pleier når vi jobber med grafikk.
# pig_main.py
from uib_inf100_graphics.simple import canvas, display
from pig_head import draw_head
from pig_body import draw_body
# TODO: kall på funksjonene draw_body og draw_head
...
display(canvas)
På de første linjene importerer du fra ulike kilder: uib_inf100_graphics.simple er et eksternt bibliotek du har installert, mens pig_head og pig_body er .py -filer som ligger i samme mappe som din egen fil. Det ser veldig likt ut i koden fordi det er veldig likt: det eksterne biblioteket er en .py -fil det også (bare at den ligger i en skjult mappe knyttet til Python-fortolkeren din).
For å gjøre ferdig oppgaven, må du utføre kall til draw_head og draw_body -funksjonene du nettopp har importert. Du må gjøre deg kjent med hvilke parametre disse funksjonene forventer ved å lese litt i filene til Ola og Kari. Når du er ferdig, skal du kunne kjøre pig_main.py og få et vindu som ser omtrent slik ut:

Korteste ord (JSON)
I filen shortest_words.py, skriv et program som leser inn nøyaktig 3 ord fra en fil shortest_words.json og skriver ut det korteste ordet. Om flere ord har den korteste lengden skal programmet skrive ut alle de korteste ordene (i samme rekkefølge som de opptrer i filen).
Eksempler på innhold i shortest_words.json og tilhørende riktig utskrift:
{
"words": [
"Game",
"Action",
"Champion"
]
}
Game
{
"words": [
"orange",
"apple",
"grape"
]
}
apple
grape
{
"words": [
"Four",
"Five",
"Nine"
]
}
Four
Five
Nine
-
Lese en JSON-fil med Python i notatene om JSON.
-
Dype oppslag i notatene om JSON.
-
Strenger i notatene kom i gang (herunder å finne lengden til strenger).
-
Python som en enkel kalkulator i notatene kom i gang (herunder å finne minste verdi).
-
Notatene om betingelser.
-
Begynn med å finne ut hva som er den korteste lengden blant de tre ordene.
-
Bruk betingelser for å sjekke hvert av ordene, om dette ordets lengde er lik den korteste lengden. Hvis ja, skriv ut ordet.
Lengste ord (JSON)
I filen longest_word.py skal du lage et program som leser inn nøyaktig 3 ord fra en fil longest_word.json og skriver ut det lengste ordet. Men om flere ord har den lengste lengden skal programmet bare skrive ut det første ordet som har en lengste lengde.
Eksempler på innhold i longest_word.json og tilhørende riktig utskrift:
{
"words": [
"Game",
"Action",
"Champion"
]
}
Champion
{
"words": [
"pear",
"apple",
"grape"
]
}
apple
{
"words": [
"Four",
"Five",
"Nine"
]
}
Four
-
Lese en JSON-fil med Python i notatene om JSON.
-
Dype oppslag i notatene om JSON.
-
Strenger i notatene kom i gang (herunder å finne lengden til strenger).
-
Python som en enkel kalkulator i notatene kom i gang (herunder å finne største verdi).
-
Notatene om betingelser.
Overlappende sirkler
I denne oppgaven skal du skrive et program som avgjør hvorvidt to sirkler overlapper. En sirkel kan beskrives ved hjelp av et koordinat for sirkelens sentrum \((x, y)\), samt en radius \(r\).
 |
Opprett en funksjon circles_overlap(x1, y1, r1, x2, y2, r2) i filen circles_overlap.py. La funksjonen returnere True dersom to sirkler beskrevet med henholdsvis x1, y1, r1 og x2, y2, r2 overlapper, og False hvis ikke.
To sirkler overlapper dersom avstanden mellom sirklenes sentrum er mindre enn eller lik summen av sirklenes radiuser.
For å finne avstanden mellom to punkter \((x_1, y_1)\) og \((x_2, y_2)\) i et koordinatsystem, kan du bruke formelen avbildet her:

For å teste funksjonen du har skrevet kan du legge til disse linjene nederst i circles_overlap.py:
def test_circles_overlap():
print('Testing circles_overlap...', end='')
# Sirkel1 med sentrum (0, 0) og radius 1
# Sirkel2 med sentrum (1, 1) og radius 1
# Overlapper
assert circles_overlap(0, 0, 1, 1, 1, 1) is True
# Sirkel1 med sentrum (0, 0) og radius 2
# Sirkel2 med sentrum (4, 1) og radius 2
# Overlapper ikke
assert circles_overlap(0, 0, 2, 4, 1, 2) is False
# Sirkel1 med sentrum (0, 0) og radius 3
# Sirkel2 med sentrum (5, 0) og radius 2
# De overlapper hverandre i et enkelt punkt
assert circles_overlap(0, 0, 3, 5, 0, 2) is True
print('OK')
test_circles_overlap()
Illustrasjon av testene:
 |
Skuddår
Regelen for å beregne om et år er et skuddår eller ikke er som følger:
- Vanligvis er et år som er delelig med 4 et skuddår (for eksempel 1996 var et skuddår);
- bortsett fra år som også er delelige med 100 (for eksempel 1900 er ikke skuddår);
- men hvis året som er delelige med 100 også er delelig med 400, da er det et skuddår likevel (for eksempel er 2000 et skuddår).
I filen leapyear.py opprett en funksjon is_leap_year(year) som tar inn et årstall og returnerer True dersom det er et skuddår, og False hvis ikke.
Test koden din (husk at testene bare kjøres dersom du i tillegg legger inn et funksjonskall til test_is_leap_year i hovedprogrammet):
def test_is_leap_year():
print('Tester is_leap_year... ', end='')
assert is_leap_year(2022) is False # Ikke delelig med 4
assert is_leap_year(1996) is True # Normalt skuddår
assert is_leap_year(1900) is False # Delbart med 100
assert is_leap_year(2000) is True # Delbart med 400
print('OK')
-
Benytt modulo-operatøren (
%) for å avgjøre om et heltall er delelig med et annet.
PS: Hvis alt er som det skal, vil programmet skrive ut
Tester is_leap_year... OKnår det kjøres
Punkt i rektangel
Et hyperrektangel er et rektangel hvor sidene er vannrette og loddrette (ikke rotert). Vi kan representere et hyperrektangel med to koordinater \((x_1, y_1)\) og \((x_2, y_2)\) som representerer to diagonalt motsatte hjørner (du kan ikke anta noe om hvilken rekkefølge disse punktene kommer i, eller hvilke to motsatte hjørner i rektangelet de beskriver). I denne oppgaven skal du avgjøre hvorvidt et tredje punkt \((x_p, y_p)\) befinner seg innenfor et slikt rektangel eller ikke.
I en fil point_in_rectangle.py, skriv en funksjon point_in_rectangle som har seks parametre x1, y1, x2, y2, xp, yp, hvor de fire første parametrene representerer et hyperrektangel, og de to siste representerer et vilkårlig punkt. La metoden returnere True dersom punktet er innenfor rektangelet, og False hvis ikke. Dersom punktet befinner seg akkurat på linjen, regner vi det som at den er innenfor.

Test koden din (husk å at du også må legge inn et funksjonskall til denne test-funksjonen nederst i filen for å faktisk utføre testene):
def test_point_in_rectangle():
print('Tester point_in_rectangle... ', end='')
assert point_in_rectangle(0, 0, 5, 5, 3, 3) is True # Midt i
assert point_in_rectangle(0, 5, 5, 0, 5, 3) is True # På kanten
assert point_in_rectangle(0, 0, 5, 5, 6, 3) is False # Utenfor
print('OK')
-
Omregn rektangelet slik at du vet hva som er høyre og venstre, top og bunn. For eksempel, opprett variabler
x_left = min(x1, x2)ogx_right = max(x1, x2). Tilsvarende for topp og bunn med y-aksen. -
Sjekk at punktet \((x_p, y_p)\) både befinner seg mellom venstre- og høyresiden, og også mellom topp og bunn.
-
For eksempel: punktet \((x_p, y_p)\) er mellom høyre- og venstre siden dersom både
x_lefter mindre eller likxpogxper mindre eller likx_right.
Belgisk flagg
I denne oppgaven skal vi lage en funksjon som tegner et belgisk flagg.
Opprett filen belgian_flag.py med en funksjon draw_belgian_flag som har fem parametere: canvas, x1, y1, x2, y2. Funksjonen skal tegne et belgisk flagg på canvas med øvre venstre hjørne i punktet \((x_1, y_1)\) og nedre høyre hjørne i punktet \((x_2, y_2)\). Funksjonen trenger ikke å ha noen retursetning.
# belgian_flag.py
def draw_belgian_flag(canvas, x1, y1, x2, y2):
# TOOD: replace this function body with code to draw the Belgian flag
...
Merk: du skal ikke importere noe i belgian_flag.py. Når du kjører filen forventer vi heller ikke at noe skjer, siden programmet ikke inneholder noen kall til funksjonen. For å teste at funksjonen din fungerer, kan du i stedet opprette en ny fil belgian_flag_test.py i samme mappe og kopiere inn dette programmet:
# belgian_flag_test.py
from uib_inf100_graphics.simple import canvas, display
from belgian_flag import draw_belgian_flag
draw_belgian_flag(canvas, 125, 135, 275, 265)
draw_belgian_flag(canvas, 10, 10, 40, 36)
draw_belgian_flag(canvas, 10, 340, 390, 360)
display(canvas)
Om du har gjort alt riktig i belgian_flag.py og deretter kjører belgian_flag_test.py, skal det tegnes tre belgiske flagg som vist under:

Innramming
Opprett filen frame.py og kopier inn følgende kode:
|
|
Legg også inn frame_word_test.json i samme mappe.
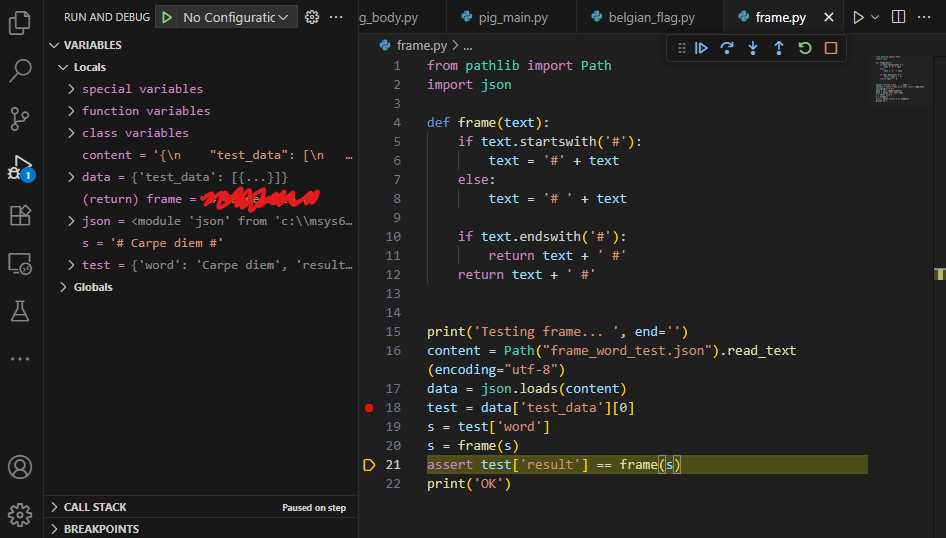
Om du kjører koden, vil du oppdage at programmet krasjer på linje 21 med en AssertionError. Vi skjønner at noe er galt, men vi vet ikke hva. Vi skal nå benytte debuggeren for å se hvilken returverdi vi faktisk får i funksjonskallene på linje 21.
- Sett et breakpoint på linje 18 eller 19 og kjør programmet i debug-modus. Bruk step over -knappen for å gå noen steg, helt til neste linje som skal utføres (den markerte linjen) er linje 21.
- Undersøk variabel-området i debuggeren. Legg merke til hva
ser nå. - Siden alt ser bra ut, fortsetter vi: trykk på step into for å gå inn i funksjonskallet til frame.
- Her kunne du trykket på «step over» for å gå steg for steg gjennom setningene i funksjonskroppen; men akkurat nå er vi er mest interessert i selve returverdien, så trykk i stedet på step out.
- Undersøk variabel-området i debuggeren på nytt. Legg merke til at det er en «variabel» der som heter
(return) frame. Denne viser til returverdien fra funksjonskallet vi nettopp gikk ut fra. Hva er det som er feil?
Ta et skjermbilde frame_debug.png av debuggeren som viser variabel-området i debuggeren og hvilken verdi (return) frame har. Last opp dette bildet som besvarelse på denne oppgaven.
PS: For å kunne se returverdien må du benytte deg av «step out» -knappen. Om du benytter en av de andre knappene når du forlater funksjonskroppen kan det være du utløser assert-krasjen.
Vi forventer at skjermbildet du leverer ser omtrent slik ut (men selvfølgelig uten sladden):
Forklar for deg selv: hva er forskjellen på «step over» og «step into»?
Bonus: hvilken return-setning ble utført? Start debuggeren på nytt og gå steg for steg gjennom funksjonskroppen helt til du ser hvilken return-setning som utføres. Feilen ligger kanskje her? Fiks feilen slik at testen passerer.
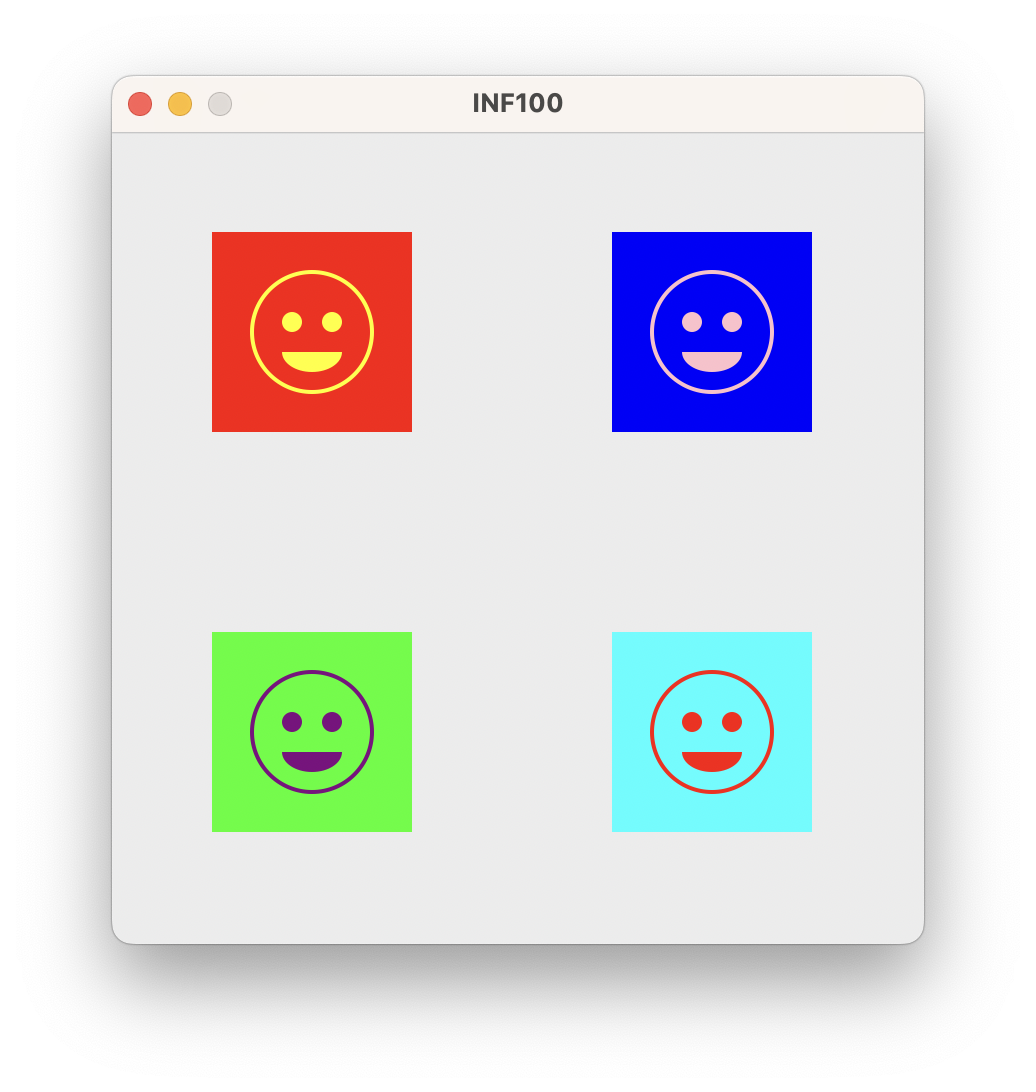
Ansikt
Før du gjør denne oppgaven, må du installere grafikk-biblioteket vi benytter i emnet. Se instruksjoner i kursnotater om grafikk.
I filen face.py, skriv kode som tegner et ansikt. Du kan velge helt selv hvordan ansiktet ser ut. Du må benytte uib_inf100_graphics.simple når du tegner. Noen eksempler:


Når du leverer denne oppgaven på CodeGrade, vil et skjermbilde av programmet ditt automatisk lastes opp til galleriet hvor du også kan se dine medstudenter sine besvarelser.
Siste lengste ord (JSON)
I filen last_longest_word.py skal du lage et program som leser inn nøyaktig 3 ord fra en fil last_longest_word.json og skriver ut det lengste ordet. Men om flere ord har den lengste lengden skal programmet bare skrive ut det siste ordet som har en lengste lengde.
Eksempler på innhold i longest_word.json og tilhørende riktig utskrift:
{
"words": [
"Game",
"Action",
"Champion"
]
}
Champion
{
"words": [
"pear",
"apple",
"grape"
]
}
grape
{
"words": [
"Four",
"Five",
"Nine"
]
}
Nine
-
Lese en JSON-fil med Python i notatene om JSON.
-
Dype oppslag i notatene om JSON.
-
Strenger i notatene kom i gang (herunder å finne lengden til strenger).
-
Python som en enkel kalkulator i notatene kom i gang (herunder å finne største verdi).
-
Notatene om betingelser.
Kollisjonsdeteksjon
Denne oppgaven består av to deler. Skriv funksjoner til begge deloppgaver (A-B) i én felles fil, collision_detection.py.
Del A
I filen collision_detection.py, skriv en funksjon rectangles_overlap som har åtte parametre x1, y1, x2, y2, x3, y3, x4, y4, hvor de fire første parametrene ett hyperrektangel, og de fire siste representerer et annet (et hyperrektangel representeres av to motsatte hjørner, men vi kan ikke gjøre noen ytterligere antakelser om hvilke hjørner). La metoden returnere True dersom rektanglene overlapper hverandre, og False hvis ikke. Vi sier at rektanglene overlapper selv om de kun deler ett enkelt punkt.

Test koden din:
def test_rectangles_overlap():
print('Tester rectangles_overlap... ', end='')
assert rectangles_overlap(0, 0, 5, 5, 2, 2, 6, 6) is True # Delvis overlapp
assert rectangles_overlap(0, 5, 5, 0, 1, 1, 4, 4) is True # Fullstendig overlapp
assert rectangles_overlap(0, 1, 7, 2, 1, 0, 2, 7) is True # Kryssende rektangler
assert rectangles_overlap(0, 5, 5, 0, 5, 5, 7, 7) is True # Deler et hjørne
assert rectangles_overlap(0, 0, 5, 5, 3, 6, 5, 8) is False # Utenfor
print('OK')
- Omregn begge rektangler slik at du vet hva som er høyre og venstre, top og bunn (se hint for oppgaven “Punkt i rektangel”").
- Dersom høyresiden til ett rektangel er til venstre for venstresiden av det andre, blir svaret false (tilsvarende logikk med topp og bunn). Husk å sjekke begge retninger.
Illustrasjon av testcasene i assert’ene over:

Del B
I filen collision_detection.py, skriv en funksjon circle_overlaps_rectangle som har syv parametre x1, y1, x2, y2, xc, yc, rc, hvor de fire første parametrene representerer to motstående hjørner i et hyperrektangel, og de tre siste representerer en sirkel sentrert i \((x_c, y_c)\) med radius \(r_c\). La metoden returnere True dersom sirkelen overlapper rektangelet, og False hvis ikke. Dersom sirkelen og rektangelet deler kun ett enkelt punkt regnes det fremdeles som at de er overlappende.

Test koden din:
def test_circle_overlaps_rectangle():
print('Tester circle_overlaps_rectangle... ', end='')
assert circle_overlaps_rectangle(0, 0, 5, 5, 2.5, 2.5, 2) is True # på midten
assert circle_overlaps_rectangle(0, 5, 5, 0, 8, 3, 2) is False # langt utenfor
assert circle_overlaps_rectangle(0, 0, 5, 5, 2.5, 7, 2.01) is True # på kanten
assert circle_overlaps_rectangle(0, 5, 5, 0, 5.1, 5.1, 1) is True # på hjørnet
assert circle_overlaps_rectangle(0, 0, 5, 5, 8, 8.99, 5) is True # på hjørnet
assert circle_overlaps_rectangle(0, 0, 5, 5, 8, 9.01, 5) is False # bare nesten
print('OK')
- Dersom sirkelens sentrum er inne i rektangelet, er svaret
True. Bruk funksjonen du skrev i oppgaven om punkt i rektangel for å sjekke dette.- Du kan importere funksjonen ved å legge til
from point_in_rectangle import point_in_rectangleøverst i collision_detection.py.
- Du kan importere funksjonen ved å legge til
- La det minste x-koordinatet av
x1ogx2kallesx_left, og la det største kallesx_right. På samme måte, slutt å tenke på punkteney1ogy2, og regn i stedet ut punkteney_topogy_bottom. - «Utvid» rektangelet med sirkelens radius i alle retninger. Hvis sirkelens sentrum er utenfor dette utvidede rektangelet (bruk funksjonen point_in_rectangle igjen), er det garantert ikke noe overlapp.
- I de gjenstående tilfellene befinner sirkelen sitt sentrum seg i rammen rundt rektangelet som er tegnet med stiplet linje i illustrasjonen over.
- Dersom sirkelens x-koordinat befinner seg mellom x-koordinatene til det opprinnelige rektangelet, er det overlapp.
- Tilsvarende for y-aksen.
- Hvis sirkelens sentrum ikke tilfredsstiller noen av de to punktene over, befinner det seg i et av hjørnene. Dersom sirkelens sentrum har større avstand enn \(r_c\) til samtlige hjørner i det opprinnelige rektangelet, er det ingen overlapp (f. eks. slik som på figuren over). For å finne avstanden, bruk funksjonen distance som du kan importere fra en tidligere oppgave (
from distance import distance).
Illustrasjon av testcasene oppgitt over (en sirkel per testcase):


if point_in_rectangle(...): # sirkelens sentrum inne i rektangel?
return True
elif not point_in_rectange(...): # sentrum utenfor utvidet rektangel?
return False
elif ... # punkt er mellom venstre og høyresiden til rektangel (x-aksen)
return True
elif ... # punkt er mellom topp og bunn til rektangel (y-aksen)
return True
elif distance(...) # sirkelen overlapper hjørnet oppe til venstre
return True
elif ... # sirkelen overlapper hjørnet oppe til høyre
return True
...
